
分析 (1)用待定系数法求二次函数的解析式即可;
(2)求得顶点D的坐标,根据PE的长,可得出点P的坐标,过点P作x轴的垂线,垂足为O,证明四边形PEHQ为矩形,即可得出d与m之间的函数关系式;
(3)连接PF,可得点E的坐标,再根据勾股定理得出EF的长,连接OG交DH,证明△OCG≌△OBG,即可得出直线OT、BD、CG的解析式,根据点P在直线CG上,得出点P的坐标,再求得点N的坐标.
解答 解:(1)依题意可得,点B、C的坐标为(3,0),(0,3);
∵OB=3OA,点A在x轴的负半轴上,
∴点A的坐标为(-1,0),
根据题意得$\left\{\begin{array}{l}{0=a×{3}^{2}+b×3+3}\\{0=a×(-1)^{2}+b×(-1)+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴所求抛物线的解析式为y=-x2+2x+3;
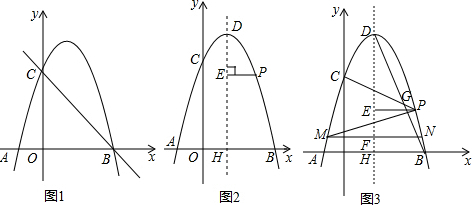
(2)如图1,由(1)中的抛物线可知,顶点D的坐标为(1,4),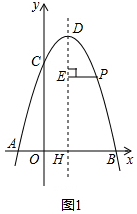
∴DH=4,
∵点P在抛物线上,PE与对称轴垂直,PE=m,
∴点P的横坐标为m+1,代入抛物线解析式得y=-(m+1)2+2(m+1)+3=-m2+4,
∴点P的坐标为(m+1,-m2+4),
过点P作x轴的垂线,垂足为Q,
∵∠PEH=∠PQH=∠EHQ=90°,
∴四边形PEHQ为矩形,
∴EH=PQ=-m2+4,
∴d=DE=DH-EH=4-(-m2+4)=m2;
(3)如图2,连接PF,
由(2)可知点E的坐标为(1,-m2+4),
设FM=FN=n,可知点N坐标为(n+1,-n2+4),
∴点F坐标为(1,-n2+4),
∴EF=(-m2+4)-(-n2+4)=n2-m2,
∵∠MPN=90°,F是斜边MN的中点,
∴PF=FN=n,
在Rt△PEF中,由勾股定理可得PE2+EF2=PF2,
∴m2+(n2-m2)2=n2,
∴(n2-m2)2=n2-m2,
∴EF2=EF,
∴EF=1,
连接OG交DH于点T,
在△OCG和△OBG中,$\left\{\begin{array}{l}{OC=OB}\\{OG=OG}\\{CG=BG}\end{array}\right.$,
∴△OCG≌△OBG,
∴∠GOC=∠GOB=45°,
∴TH=OH=1,
∴T(1,1),
∴直线OT的解析式为y=x,
∴点G在直线y=x上;
设直线BD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{4=k+b}\\{0=3k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴直线BD的解析式为y=-2x+6,
∵点G在BD上,∴点G的坐标为(2,2),
设直线GC的解析式为y=k1x+b1,
∴$\left\{\begin{array}{l}{3={b}_{1}}\\{2=2{k}_{1}+{b}_{1}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-\frac{1}{2}}\\{{b}_{1}=3}\end{array}\right.$,
∴直线CG的解析式为y=-$\frac{1}{2}$x+3,
∵点P在直线CG上,∴可设点P的坐标为(x,-$\frac{1}{2}$x+3),
∴-$\frac{1}{2}$x+3=-x2+2x+3,
解得x1=0(舍去),x2=$\frac{5}{2}$;
∴满足要求的点P的坐标为($\frac{5}{2}$,$\frac{7}{4}$),
∴$\frac{7}{4}$-1=$\frac{3}{4}$,
∴-n2+4=$\frac{3}{4}$,
∵n>0,
∴n=$\frac{\sqrt{13}}{2}$,
∴点N坐标为($\frac{\sqrt{13}}{2}$+1,$\frac{3}{4}$).
点评 本题考查了二次函数的相关性质、一次函数的相关性质、一元二次方程根与系数的关系以及二次根式的运算、平行四边形、全等三角形等.本题综合性较强、考查知识点较多、难度较大,注重了知识与能力的考查.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
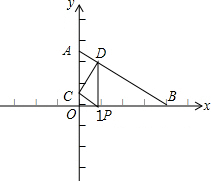 已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D
已知直角三角形纸片OAB,其中∠AOB=90°,OA=3,OB=4,点P(t,0)是OB边上的动点,过点P作PC∥AB交y轴于点C,同时过点P作PD⊥x轴交AB于点D查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
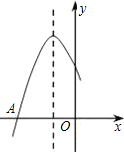 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是①④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
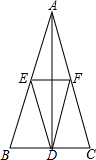 文文画了一个等腰△ABC,如图,AB=AC,他又画出BC边上的高AD,在AB上任取一点E过点E作EF∥BC,交AC于点F,然后他写下两个结论.
文文画了一个等腰△ABC,如图,AB=AC,他又画出BC边上的高AD,在AB上任取一点E过点E作EF∥BC,交AC于点F,然后他写下两个结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com