考点:勾股定理的逆定理
专题:证明题
分析:利用已知条件求出a=16,或b=16,或c=16,由a+b+c=32,得出b+c=a,或a+c=b,或a+b=c,根据勾股定理的逆定理即可证明以
,
,
为三边长可构成一个直角三角形.
解答:
证明:将①代入②,得
+
+
=
,
两边同乘abc,整理得,1024-2(a
2+b
2+c
2)=
abc ③,
由①得(a+b+c)
2=1024,即a
2+b
2+c
2=1024-2(ab+bc+ca),
代入③,得1024-2[1024-2(ab+bc+ca)]=
abc,
即abc=16(ab+bc+ca)-4096,
(a-16)(b-16)(c-16)=abc-16(ab+bc+ca)+256(a+b+c)-16
3=-4096+256×32-16
3=0,
所以a=16,或b=16,或c=16,
∵a+b+c=32,
∴b+c=a,或a+c=b,或a+b=c,
∴以
,
,
为三边长可构成一个直角三角形.
点评:本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.同时考查了分式的运算,求出a=16,或b=16,或c=16是解题的关键.本题的计算难度较大.



 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程.
如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BC,AE∥BD.请完成下列证明过程. 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )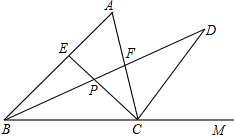 如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.
如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.