
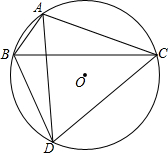
 如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
|
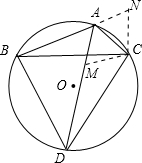 ∴△ABC≌△MDC(AAS),
∴△ABC≌△MDC(AAS),

科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、60人 | B、55人 |
| C、50人 | D、45人 |
查看答案和解析>>
科目:初中数学 来源: 题型:
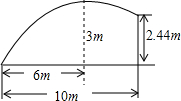 如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?
如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com