练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知S1=1，S2=3，S3=2，S4=4，求S5、S6、S7的值．
    考点：勾股定理
    专题：
    分析：直接根据勾股定理即可得出结论．
    解答：解：∵图形中的三角形均是直角三角形，S1=1，S2=3，S3=2，S4=4，
    ∴S5=S1+S2=1+3=4，S6=S3+S4=2+4=6，S7=S5+S6=4+6=10．
    点评：本题考查的是勾股定理，这是著名的勾股树，要熟悉勾股定理的几何意义．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    计算：（下列各题解答时必须给出必要的演算过程或推理步骤）
    （1）（-20）+（-3）-（-5）-（+7）
    （2）-5+6÷（-2）×
    1
    3

    （3）（-1）100×|-5|-4×（-3）-42 
    （4）3x2-[7x-3（4x-3）-2x2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知BD、CE是△ABC的中线，M、N分别是BD、CE的中点，那么MN：BC=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E，求证：BD=BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，∠C=90°，AC=BC，AD是∠A的平分线，交CB于点D．
    （1）求证：AB=AC+CD；
    （2）若AC=3，求BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，海岛B位于港口A的西南方向，19：00时，甲船从港口A出发，以18海里/小时的速度先沿正西方向航行1小时到达港口C装载物资，半小时后再转向南偏西30°方向开往海岛B，结果22：30到达．  
    （1）求甲船从港口C驶向海岛B的速度（精确到0.1海里/小时）． 
    （2）在甲船从港口A出发的同时，乙船也从港口A出发以18海里/小时的速度直接开往海岛B，已知海岛B处有一座灯塔，在离灯塔方圆5海里内都可以看见灯塔，问甲、乙两船在航行途中哪一艘船先看到灯塔？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

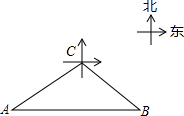    已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行，30min后到港口B，又从港口B以同样的速度15min后航行到港口C，此时在C处测得港口A位于港口C的南偏西63.4°方向上，求该艘轮船以80km∕h的速度返回到港口A所需的时间．（精确到0.01h，参考数据：cos63.4°≈0.45，sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50，
    		2
    ≈1.41，
    		5
    ≈2.24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

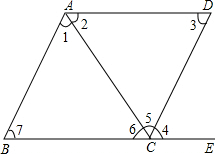    如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．
    （1）∵∠1=∠5（已知），
    ∴
     
    ∥
     
    （
     
    　
    （2）∵∠2=∠6（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （3）∵∠4=∠7（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （4）∵∠3=∠4（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （5）∵∠3+∠BCD=180°（已知），
    ∴
     
    ∥
     
    （
     
    　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB是⊙O的弦，P是线段AB上一动点，OP长度满足2≤OP≤3，则AB=
     
    ．

    查看答案和解析>>

    同步练习册答案