
【题目】某商场开业后经历了从亏损到盈利的过程,图像刻画了该店开业以来累计利润![]() (万元)与开业时间
(万元)与开业时间![]() (月)之间的关系(累计利润是指前
(月)之间的关系(累计利润是指前![]() 个月利润总和).
个月利润总和).
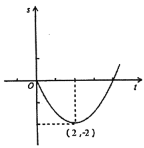
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)截止到第几个月,累计利润可达16万元?
(3)求第9个月的利润.
【答案】(1)S=![]() t2﹣2t;(2)截止到第8个月公司累积利润可达30万元;(3)第9个月的利润是6.5万元.
t2﹣2t;(2)截止到第8个月公司累积利润可达30万元;(3)第9个月的利润是6.5万元.
【解析】
(1)本题是通过构建函数模型解答销售利润的问题,应根据图象以及题目中所给的信息来列出S与t之间的函数关系式;
(2)把S=30代入累计利润S=![]() t2﹣2t的函数关系式里,求得月份;
t2﹣2t的函数关系式里,求得月份;
(3)分别把t=9,t=8,代入函数解析S=![]() t2﹣2t,再把总利润相减就可得出.
t2﹣2t,再把总利润相减就可得出.
解(1)设其函数关系式为:S=a(t﹣2)2﹣2.
∵所求函数关系式的图象过(0,0),
代入得:
a(0﹣2)2﹣2=0,
解得a=![]() ,
,
∴所求函数关系式为:S=![]() (t﹣2)2﹣2,即S=
(t﹣2)2﹣2,即S=![]() t2﹣2t.
t2﹣2t.
答:累积利润S与时间t之间的函数关系式为:S=![]() t2﹣2t;
t2﹣2t;
(2)把S=16代入S=![]() (t﹣2)2﹣2,
(t﹣2)2﹣2,
得 ![]() (t﹣2)2﹣2=16.
(t﹣2)2﹣2=16.
解得t1=8,t2=﹣4(舍去).
答:截止到第8个月公司累积利润可达30万元.
(3)把t=9代入关系式,
得S=![]() ×92﹣2×9=22.5,
×92﹣2×9=22.5,
由(2)可知t=8时,累计利润16万元
22.5﹣16=6.5,
答:第9个月的利润是6.5万元.


科目:初中数学 来源: 题型:
【题目】“国际无烟日”来临之际,小明就公众对在餐厅吸烟的态度进行了调查,并将调查结果制作成如图所示的统计图,请你根据图中信息回答:

(1)被调查者中,不吸烟者赞成在餐厅彻底禁烟的人数是 .
(2)被调查者中,希望在餐厅设立吸烟室的人数是 .
(3)求被调查者中赞成在餐厅彻底禁烟的频率.
(4)眉山市现有人口约380万,根据图中信息估计眉山市现有人口中赞成在餐厅彻底禁烟的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)证明该方程一定有两个不相等的实数根;
(2)设该方程两根为x1、x2(x1<x2).
①当![]() 时,试确定y值的范围;
时,试确定y值的范围;
②如图,平面直角坐标系中有三点A、B、C,坐标分别为(x1,0)、(x2,3)、(7,0).以点C为圆心,2个单位长度为半径的圆与直线AB相切,求n的值.
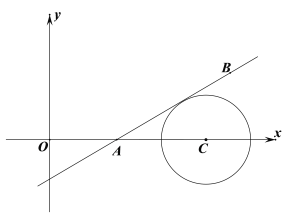
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两位同学在足球场上游戏,两人的运动路线如图1所示,其中AC=DB,小王从点A出发沿线段AB运动到点B,小林从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示,结合图象分析,下列说法正确的是( )
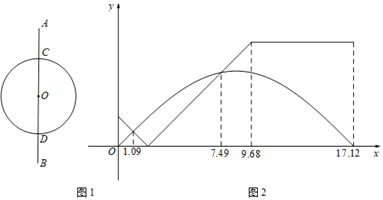
A. 小王的运动路程比小林的长
B. 两人分别在![]() 秒和
秒和![]() 秒的时刻相遇
秒的时刻相遇
C. 当小王运动到点D的时候,小林已经过了点D
D. 在![]() 秒时,两人的距离正好等于
秒时,两人的距离正好等于![]() 的半径
的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 两边的中点,如果
两边的中点,如果![]() 上的所有点都在
上的所有点都在![]() 的内部或边长,则称
的内部或边长,则称![]() 为
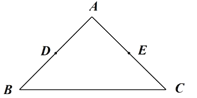
为![]() 的中内弧.例如下图中
的中内弧.例如下图中![]() 是
是![]() 的一条中内弧.
的一条中内弧.
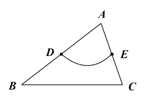
(1)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.画出
的中点.画出![]() 的最长的中内弧
的最长的中内弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点.
的中点.
①若![]() ,直接写出
,直接写出![]() 的中内弧
的中内弧![]() 所在圆的圆心
所在圆的圆心![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;
②若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,直接写出
的内部或边长,直接写出![]() 的取值范围;
的取值范围;
③若在![]() 中存在一条中内弧
中存在一条中内弧![]() ,使得
,使得![]() 所在圆的圆心
所在圆的圆心![]() 在
在![]() 的内部或边长,则
的内部或边长,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
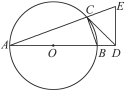
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一种水果的成本价是5元/千克,在销售中发现,当这种水果的价格定为7元/千克时,每天可以卖出160千克,在此基础上,这种水果的单价每提高1元/千克,该水果店每天就会少卖出20千克,设这种水果的单价为![]() 元(
元(![]() ),
),
(1)请用含![]() 的代数式表示:每千克水果的利润 元及每天的销售量 千克.
的代数式表示:每千克水果的利润 元及每天的销售量 千克.
(2)若该水果店一天销售这种水果所获得的利润是420元,为了让利于顾客,单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
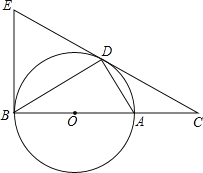
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com