Question

19．如图，在平面直角坐标系中，点M、B的坐标分别为（6，8）、（24，0），过点O作⊙M，C、D为⊙M上两点，$\widehat{OC}$=$\widehat{OA}$，E是BD中点．
（1）判断AE与AC的数量关系，并说明理由；
（2）设F是AC的中点，P为⊙M上一点，且PF=PE，求点P的坐标；
（3）是否存在点C，使AE与⊙M相切？如果存在，求点C的坐标；如果不存在，请说明理由．

Answer 1

分析 （1）作MH⊥OA于H，连结OD，如图1，由垂径定理得到OH=AH，则OA=2OH=12，于是可判断点A为OB的中点，所以AE为△OBD的中位线，则AE=$\frac{1}{2}$OD，再根据圆心角、弧、弦的关系得到AC=OD，所以AE=$\frac{1}{2}$AC；
（2）如图2，作MH⊥OA于H，连结OD、PA，根据圆心角、弧、弦的关系，由$\widehat{OC}$=$\widehat{AD}$得∠OAC=∠AOD，由AE∥OD得到∠EAB=∠AOD，则∠OAC=∠EAB，接着证明△PAF≌△PAE得到∠PAF=∠PAE，所以∠PAO=∠PAB=90°，连结OP，如图2，根据圆周角定理可判断OP为⊙M的直径，所以PA=2MH=16，于是得到P点坐标为（12，16）；
（3）如图3，作MH⊥OA于H，DQ⊥AB于Q，连结OD、DA、AM，OD交AM于N，假设AE为⊙M的切线，根据切线的性质得MA⊥AE，则AE∥OD，AE=$\frac{1}{2}$OD，所以AM⊥OD，根据垂径定理得ON=DN，接着判断四边形AEDN为矩形得到∠ODB=90°，由AN垂直平分OD得到AD=AO=12，∠DAN=∠MAH，然后证明△DAN∽△MAH，利用相似比可计算出DN=$\frac{48}{5}$，则OD=2DN=$\frac{96}{5}$，于是利用勾股定理，在Rt△ODB中可计算出BD=$\frac{72}{5}$，利用面积法可计算出DQ=$\frac{288}{25}$，再在Rt△ODQ中利用勾股定理计算出OQ=$\frac{384}{25}$，则Q点坐标为（$\frac{384}{25}$，$\frac{288}{25}$），最后利用点C与点D关于直线x=6对称可得到C点坐标．

解答 解：（1）AE=$\frac{1}{2}$AC．理由如下：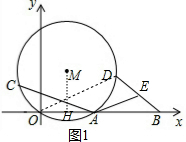
作MH⊥OA于H，连结OD，如图1，
∵MH⊥OA，
∴OH=AH，
∵M（6，8），
∴OH=6，
∴OA=2OH=12，
∵B（12，0），
∴点A为OB的中点，
∵E是BD中点，
∴AE为△OBD的中位线，
∴AE=$\frac{1}{2}$OD，
∵$\widehat{OC}$=$\widehat{AD}$，
∴$\widehat{OC}$+$\widehat{OA}$=$\widehat{AD}$+$\widehat{OA}$，即$\widehat{AC}$=$\widehat{OD}$，
∴AC=OD，
∴AE=$\frac{1}{2}$AC；
（2）如图2，作MH⊥OA于H，连结OD、PA，
∵$\widehat{OC}$=$\widehat{AD}$，
∴∠OAC=∠AOD，
∵AE为△OBD的中位线，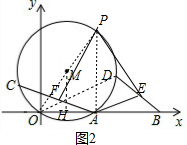
∴AE∥OD，
∴∠EAB=∠AOD，
∴∠OAC=∠EAB，
∵F是AC的中点，AE=$\frac{1}{2}$AC，
∴AF=AE，
在△PAF和△PAE中，
$\left\{\begin{array}{l}{PF=PE}\\{PA=PA}\\{AF=AE}\end{array}\right.$，
∴△PAF≌△PAE，
∴∠PAF=∠PAE，
∴∠PAO=∠PAB=90°，
连结OP，如图2，则OP为⊙M的直径，
∴PA=2MH=16，
∴P点坐标为（12，16）；
（3）存在．
如图3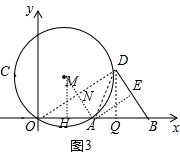，作MH⊥OA于H，DQ⊥AB于Q，连结OD、DA、AM，OD交AM于N，
假设AE为⊙M的切线，
∴MA⊥AE，
∴AE∥OD，AE=$\frac{1}{2}$OD，
∴AM⊥OD，
∴ON=DN，
∴AE=DN，
∴四边形AEDN为矩形，
∴∠ODB=90°，
∵AN垂直平分OD，
∴AD=AO=12，∠DAN=∠MAH，
∴△DAN∽△MAH，
∴DN：MH=DA：MA，即DN：8=12：10，
∴DN=$\frac{48}{5}$，
∴OD=2DN=$\frac{96}{5}$，
在Rt△ODB中，BD=$\sqrt{2{4}^{2}-（\frac{96}{5}）^{2}}$=$\frac{72}{5}$，
∵$\frac{1}{2}$DQ•OB=$\frac{1}{2}$OD•DB，
∴DQ=$\frac{\frac{96}{5}×\frac{72}{5}}{24}$=$\frac{288}{25}$，
在Rt△ODQ中，OQ=$\sqrt{（\frac{96}{5}）^{2}-（\frac{288}{25}）^{2}}$=$\frac{384}{25}$，
∴Q点坐标为（$\frac{384}{25}$，$\frac{288}{25}$），
∵$\widehat{OC}$=$\widehat{AD}$，
∴点C与点D关于直线x=6对称，
∴C点坐标为（-$\frac{84}{25}$，$\frac{288}{25}$）．

点评 本题考查了圆的综合题：熟练掌握切线的性质、垂径定理和圆心角、弧、弦的关系；会构造三角形中位线，运用三角形中位线性质得到线段之间的关系；理解坐标与图形的性质，灵活应用相似比和勾股定理进行几何计算．