
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯШЮвтвЛЕуЃЈВЛгы
ЩЯШЮвтвЛЕуЃЈВЛгы![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЕу
жиКЯЃЉЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ГѕВНИажЊЃКЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌБШНЯЃК
жиКЯЪБЃЌБШНЯЃК![]()
![]() ЃЈбЁЬюЁА
ЃЈбЁЬюЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎ
ЁБЃЉЃЎ
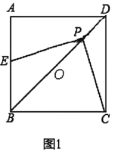
дйДЮИажЊЃКШчЭМ1ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌШчКЮХаЖЯ
ЩЯЪБЃЌШчКЮХаЖЯ![]() КЭ
КЭ![]() Ъ§СПЙиЯЕФиЃП
Ъ§СПЙиЯЕФиЃП
МзЭЌбЇЭЈЙ§Й§Еу![]() ЗжБ№Яђ
ЗжБ№Яђ![]() КЭ
КЭ![]() зїДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌжЄУїГі
зїДЙЯпЃЌЙЙдьШЋЕШШ§НЧаЮЃЌжЄУїГі![]() ЃЛ
ЃЛ
ввЭЌбЇЭЈЙ§СЌНг![]() ЃЌжЄУїГі
ЃЌжЄУїГі![]() ЃЌ
ЃЌ![]() ЃЌДгЖјжЄУїГі
ЃЌДгЖјжЄУїГі![]() ЃЎ
ЃЎ
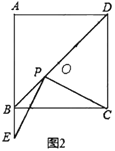
РэЯыИаЮђЃКШчЭМ2ЃЌЕБЕу![]() ТфдкЯпЖЮ
ТфдкЯпЖЮ![]() ЩЯЪБЃЌХаЖЯ
ЩЯЪБЃЌХаЖЯ![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЭиеЙгІгУЃКСЌНг![]() ЃЌВЂбгГЄ
ЃЌВЂбгГЄ![]() НЛжБЯп
НЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
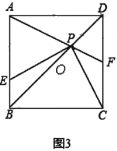
ЃЈ1ЃЉЕБ![]() ЪБЃЌШчЭМ3ЃЌжБНгаДГі
ЪБЃЌШчЭМ3ЃЌжБНгаДГі![]() ЕФУцЛ§ЮЊ ЃЛ
ЕФУцЛ§ЮЊ ЃЛ
ЃЈ2ЃЉжБНгаДГі![]() УцЛ§
УцЛ§![]() ЕФШЁжЕЗЖЮЇ ЃЎ
ЕФШЁжЕЗЖЮЇ ЃЎ
ЁОД№АИЁПГѕВНИажЊЃКЃНЃЛРэЯыИаЮђЃКPEЃНPCЃЌРэгЩМћНтЮіЃЛЭиеЙгІгУЃКЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ0ЃМSЁм
ЃЛЃЈ2ЃЉ0ЃМSЁм![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ГѕВНИажЊЃКЕБЕуPгыЕуOжиКЯЪБЃЌдђЕуEгыЕуBжиКЯЃЌИљОне§ЗНаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
РэЯыИаЮђЃКPEЃНPCЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌгЩЁАAASЁБПЩжЄЁїEGPЁеЁїPHCЃЌПЩЕУНсТлЃЛ
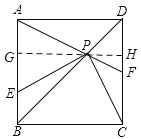
ЭиеЙгІгУЃКЃЈ1ЃЉЭЌРэзїИЈжњЯпПЩжЊЁїEGPЁеЁїPHCЃЌжЄУїЁїDPFЁзЁїBPAЃЌИљОнЯрЫЦШ§НЧаЮЯрЫЦБШЕШгкЖдгІИпЕФБШЕУЃК![]() ЃЌМЦЫуPHЃН
ЃЌМЦЫуPHЃН![]() ЃЌPGЃН
ЃЌPGЃН![]() ЃЌШЛКѓЧѓГіAEЕФГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩЕУНсТлЃЛ
ЃЌШЛКѓЧѓГіAEЕФГЄЃЌИљОнШ§НЧаЮУцЛ§ЙЋЪНПЩЕУНсТлЃЛ
ЃЈ2ЃЉЩшPHЃНxЃЌдђPGЃН9ЃxЃЌНсКЯжЎЧАЫљЕУЕФНсТлСаГіSЕФКЏЪ§ЙиЯЕЪНЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЧѓЕУSЕФШЁжЕЗЖЮЇМДПЩЃЎ
НтЃКГѕВНИажЊЃКЕБЕуPгыЕуOжиКЯЪБЃЌдђЕуEгыЕуBжиКЯЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрЁЯBCDЃН90ЁуЃЌ
ЁпЕуOЪЧBDЕФжаЕуЃЌ
ЁрOCЃНOBЃН![]() BDЃЌ
BDЃЌ
МДЃКPCЃНPEЃЌ
ЙЪД№АИЮЊЃКЃНЃЛ
РэЯыИаЮђЃКPEЃНPCЃЌРэгЩШчЯТЃК
ШчЭМ2ЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌ
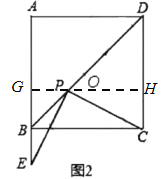
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрABЁЮCDЃЌЁЯABDЃН45ЁуЃЌЁЯAЃНЁЯABCЃН90ЁуЃЌ
ЁпGHЁЭABЃЌ
ЁрGHЁЭCDЃЌ
ЁрЁЯEGPЃНЁЯPHCЃН90ЁуЃЌ
ЁрЁЯGEPЃЋЁЯGPEЃН90ЁуЃЌ
ЁпPEЁЭPCЃЌ
ЁрЁЯEPCЃН90ЁуЃЌ
ЁрЁЯGPEЃЋЁЯCPHЃН90ЁуЃЌ
ЁрЁЯGEPЃНЁЯCPHЃЌ
ЁпЁЯABDЃН45ЁуЃЌЁЯEGPЃН90ЁуЃЌ
ЁрЁїBGPЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрBGЃНGPЃЌ
ЁпЁЯEGPЃНЁЯPHCЃНЁЯABCЃН90ЁуЃЌ
ЁрЫФБпаЮBGHCЮЊОиаЮЃЌ
ЁрBGЃНCHЃЌ
ЁрCHЃНGPЃЌ
дкЁїEGPгыЁїPHCжаЃЌ
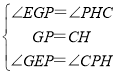
ЁрЁїEGPЁеЁїPHCЃЈAASЃЉЃЌ
ЁрPEЃНPCЃЛ
ЭиеЙгІгУЃКЃЈ1ЃЉШчЭМЃЌЙ§PзїGHЁЭABгкGЃЌНЛCDгкHЃЌ
гЩЬтвтПЩжЊЁїEGPЁеЁїPHCЃЌ
дђEGЃНPHЃЌ
ЁпЁЯAGPЃНЁЯPHDЃНЁЯADCЃН90ЁуЃЌ
ЁрЫФБпаЮAGHDЮЊОиаЮЃЌ
ЁрAGЃНDHЃЌ
ЁпЁЯBDCЃН45ЁуЃЌЁЯPHDЃН90ЁуЃЌ
ЁрЁїPHDЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрDHЃНPHЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпDCЃНABЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпABЁЮCDЃЌ
ЁрЁїDFPЁзЁїBAPЃЌ
Ёр![]() ЃЌ
ЃЌ
гжЁпGHЃНADЃН9ЃЌ
ЁрPHЃН![]() ЃЌPGЃН
ЃЌPGЃН![]() ЃЌ
ЃЌ
ЁрEGЃНDHЃНPHЃН![]() ЃЌ
ЃЌ
ЁрAGЃНDHЃН![]() ЃЌ
ЃЌ
ЁрAEЃНAGЃЋGEЃН![]() ЃЌ
ЃЌ
ЁрSЁїAPEЃН![]() ЃЌ
ЃЌ
ЙЪЁїAPEЕФУцЛ§ЮЊЃК![]() ЃЌ
ЃЌ
ЃЈ2ЃЉЩшPHЃНxЃЌдђPGЃН9ЃxЃЌ
гЩЬтвтПЩжЊЃКAGЃНEGЃНDHЃНPHЃНxЃЌ
дђSЃН![]()
![]()
![]()
![]()
Ёп0ЃМxЃМ9ЃЌ
Ёр0ЃМSЁм![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК0ЃМSЁм![]() ЃЎ
ЃЎ


 ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
ЦкФЉ1ОэЫижЪНЬг§ЦРЙРОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСае§ЖрБпаЮжаЃЌ![]() ЪЧжааФЃЌЖЈвхЃК
ЪЧжааФЃЌЖЈвхЃК![]() ЮЊЯргІе§ЖрБпаЮЕФЛљБОШ§НЧаЮЃЎШчЭМ1ЃЌ
ЮЊЯргІе§ЖрБпаЮЕФЛљБОШ§НЧаЮЃЎШчЭМ1ЃЌ![]() ЪЧе§Ш§НЧаЮ
ЪЧе§Ш§НЧаЮ![]() ЕФЛљБОШ§НЧаЮЃЛШчЭМ2ЃЌ
ЕФЛљБОШ§НЧаЮЃЛШчЭМ2ЃЌ![]() ЪЧе§ЗНаЮ
ЪЧе§ЗНаЮ![]() ЕФЛљБОШ§НЧаЮЃЛШчЭМ3ЃЌ
ЕФЛљБОШ§НЧаЮЃЛШчЭМ3ЃЌ![]() ЮЊе§
ЮЊе§![]() БпаЮ
БпаЮ![]() ЁЕФЛљБОШ§НЧаЮЃЎНЋЛљБО
ЁЕФЛљБОШ§НЧаЮЃЎНЋЛљБО![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() НЧЖШЕУ
НЧЖШЕУ![]() ЃЎ
ЃЎ
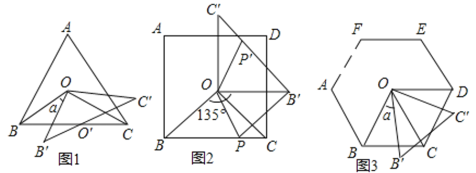
ЃЈ1ЃЉШєЯпЖЮ![]() гыЯпЖЮ
гыЯпЖЮ![]() ЯрНЛЕу
ЯрНЛЕу![]() ЃЌдђЃК
ЃЌдђЃК
ЭМ1жа![]() ЕФШЁжЕЗЖЮЇЪЧ________ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ________ЃЛ
ЭМ3жа![]() ЕФШЁжЕЗЖЮЇЪЧ________ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ________ЃЛ
ЃЈ2ЃЉдкЭМ1жаЃЌЧѓжЄ![]()
ЃЈ3ЃЉдкЭМ2жаЃЌе§ЗНаЮБпГЄЮЊ4ЃЌ![]() ЃЌБп
ЃЌБп![]() ЩЯЕФвЛЕу
ЩЯЕФвЛЕу![]() а§зЊКѓЕФЖдгІЕуЮЊ
а§зЊКѓЕФЖдгІЕуЮЊ![]() ЃЌШє
ЃЌШє![]() газюаЁжЕЪБЃЌЧѓГіИУзюаЁжЕМАДЫЪБ
газюаЁжЕЪБЃЌЧѓГіИУзюаЁжЕМАДЫЪБ![]() ЕФГЄЖШЃЛ
ЕФГЄЖШЃЛ
ЃЈ4ЃЉШчЭМ3ЃЌЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
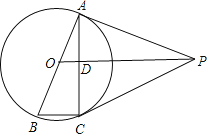
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌACЪЧЯвЃЌODЁЭACгкЕуDЃЌЙ§ЕуAзїЁбOЕФЧаЯпAPЃЌAPгыODЕФбгГЄЯпНЛгкЕуPЃЌСЌНгPCЁЂBCЃЎ
ЁО1ЁПВТЯыЃКЯпЖЮODгыBCгаКЮЪ§СПКЭЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЁО2ЁПЧѓжЄЃКPCЪЧЁбOЕФЧаЯп
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЙњЁАђдСњЁБКХЩюЧБЦїФПЧАзюДѓЩюЧБМЋЯоЮЊ7062ЃЎ68УзЃЎФГЬьИУЩюЧБЦїдкКЃУцЯТ1800УзДІзївЕЃЈШчЭМЃЉЃЌВтЕУе§ЧАЗНКЃЕзГСДЌCЕФИЉНЧЮЊ45ЁуЃЌИУЩюЧБЦїдкЭЌвЛЩюЖШЯђе§ЧАЗНжБЯпКНаа2000УзЕНBЕуЃЌДЫЪБВтЕУКЃЕзГСДЌCЕФИЉНЧЮЊ60ЁуЃЎЧыХаЖЯГСДЌCЪЧЗёдкЁАђдСњЁБКХЩюЧБМЋЯоЗЖЮЇФкЃПВЂЫЕУїРэгЩЃЛЃЈОЋШЗЕН0ЃЎ01ЃЉЃЈВЮПМЪ§ОнЃК![]() Ёж1ЃЎ414ЃЌ
Ёж1ЃЎ414ЃЌ![]() Ёж1ЃЎ732ЃЉ
Ёж1ЃЎ732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФЦНааЯпгы
ЕФЦНааЯпгы![]() ЕФЦНЗжЯпНЛгкЕу
ЕФЦНЗжЯпНЛгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉСЌНг![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФбгГЄЯпНЛгк
ЕФбгГЄЯпНЛгк![]() ЕуЃЌСЌНг
ЕуЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФГЄЮЊ ЃЎ
ЕФГЄЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
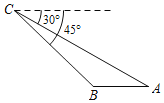
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуCДІгавЛИіИпПеЬНВтЦјЧђЃЌДгЕуCДІВтЕУЫЎЦНЕиУцЩЯAЃЌBСНЕуЕФИЉНЧЗжБ№ЮЊ30ЁуКЭ45ЁуЃЎШєAB=2kmЃЌдђAЃЌCСНЕужЎМфЕФОрРыЮЊ_____kmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
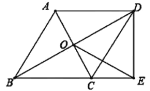
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯDЃН90ЁуЃЌADЃН4ЃЌBCЃН3ЃЎЗжБ№вдЕуAЃЌCЮЊдВаФЃЌДѓгк![]() ACГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуEЃЌЩфЯпBEНЛADгкЕуFЃЌНЛACгкЕуOЃЎШєЕуOЧЁКУЪЧACЕФжаЕуЃЌдђCDЕФГЄЮЊ__ЃЎ
ACГЄЮЊАыОЖзїЛЁЃЌСНЛЁНЛгкЕуEЃЌЩфЯпBEНЛADгкЕуFЃЌНЛACгкЕуOЃЎШєЕуOЧЁКУЪЧACЕФжаЕуЃЌдђCDЕФГЄЮЊ__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌADЃНBDЃЌЙ§ЕуDзїDEЁЭABгкЕуEЃЌЙ§ЕуAзїAHЁЭBDгкЕуHЃЌНЛDEЁЂBCЗжБ№гкЕуFЁЂGЃЌСЌНгCFЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЁЯBAGЃНЁЯFCBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуAзїAKЦНЗжЁЯDAFНЛEDгкЕуKЃЌШєAKЃН1ЃЌЁЯFCDЃН45ЁуЃЌЧѓDFЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШєADЃН10ЃЌDHЃН6ЃЌЧѓCFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2+bx+cЃЈaЃМ0ЃЉОЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЧвТњзу4a+2b+cЃО0ЃЌгаЯТСаНсТлЃКЂйa+bЃО0ЃЛЂкЉa+b+cЃО0ЃЛЂлb2Љ2acЃО5a2ЃЎЦфжаЃЌе§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 0B. 1C. 2D. 3
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com