
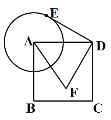
【题目】如图,已知正方形ABCD的边长为4,以点A为圆心,2为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值____.![]()
【答案】4![]() .
.
【解析】
根据题意先证明△ADE≌△CDF,则CF=AE=1,根据三角形三边关系得:AF≤AC-CF,可知:当F在AC上时,AF最小,所以由勾股定理可得AC的长,可求得AF的最小值.
解:如图,连接FC,AC,AE.
∵ED⊥DF,
∴∠EDF=∠EDA+∠ADF=90°,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADF+∠CDF=90°,
∴∠EDA=∠CDF,
在△ADE和△CDF中,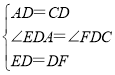
∴△ADE≌△CDF(SAS),
∴CF=AE=1,
∵正方形ABCD的边长为4,
∴AC=4![]() ,
,
∵AF≥AC-CF,
∴AF≥4![]() -2
-2
∴AF的最小值是4![]() -2;
-2;
故答案为:4![]() -2.
-2.


科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平行四边形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() ;
;
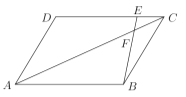
(1)如果![]() ,
,![]() ,那么请用
,那么请用![]() 、
、![]() 来表示
来表示![]() ;
;
(2)在原图中求作向量![]() 在
在![]() 、
、![]() 方向上的分向量;(不要求写作法,但要指出所作图中表示结论的向量)
方向上的分向量;(不要求写作法,但要指出所作图中表示结论的向量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
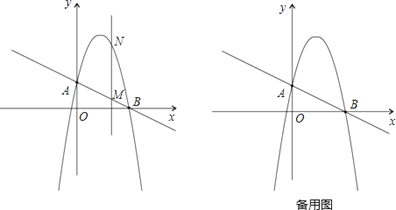
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为![]() 的三角形叫做半直角三角形.如图,在平面直角坐标系中,
的三角形叫做半直角三角形.如图,在平面直角坐标系中,![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 是
是![]() 轴上的一个动点,
轴上的一个动点,![]() (
(![]() 、
、![]() 、
、![]() 按顺时针方向排列),
按顺时针方向排列),![]() 与经过
与经过![]() 、
、![]() 、
、![]() 三点的
三点的![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() ,连结
,连结![]() ,
,![]() .显然
.显然![]() 、
、![]() 、
、![]() 是半直角三角形.
是半直角三角形.
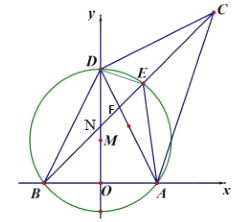
(1)求证:![]() 是半直角三角形;
是半直角三角形;
(2)求证:![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的长;
的长;
(4)![]() 交
交![]() 轴于点
轴于点![]() ,求△ACF与△BCA的面积之比.
,求△ACF与△BCA的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
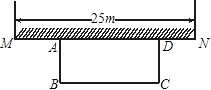
查看答案和解析>>
科目:初中数学 来源: 题型:
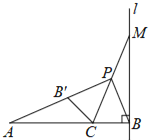
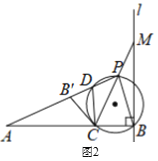
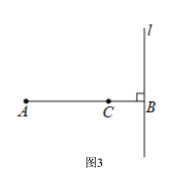
【题目】如图,直线l⊥线段AB于点B,点C在AB上,且AC=2CB,点M是直线l上的动点,作点B关于直线CM的对称点B’,直线AB’与直线CM相较于点P,联结PB.
(1)如图1,若点P与点M重合,则∠PAB=_____°,线段PA与PB的比值为______.
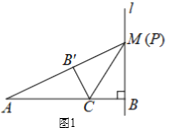
(2)如图2,若点P与点M不重合,设过P、B、C三点的圆与直线AP相交于点D,联结CD.
①求证:CD=CB’.
②求证:PA=2PB.
(3)如图③,AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB.
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com