
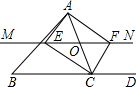
 如图,在△ABC中,O是AC上一动点(不与点A、C重合),过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
如图,在△ABC中,O是AC上一动点(不与点A、C重合),过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.分析 (1)根据角平分线的定义可得∠BCE=∠ACE,∠OCF=∠FCD,根据两直线平行,内错角相等可得∠OEC=∠BCE,∠OFC=∠FCD,然后求出∠ACE=∠OEC,∠OCF=∠OFC,再根据等角对等边可得OE=OC,同理可得OF=OC,从而得到OE=OF;
(2)当O运动到AC中点时,四边形AECF是矩形,由AO=CO,OE=OF可得四边形AECF是平行四边形,然后再证明∠ECF=90°可得四边形AECF是矩形.
解答 解:(1)OE=OF,
∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠FCD,
∵CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE,∠OCF=∠FCD,
∴∠ACE=∠OEC,∠OCF=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=$\frac{1}{2}$∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
点评 此题主要考查了矩形的判定,以及等腰三角形的判定,关键是掌握等角对等边;有一个角为直角的平行四边形是矩形.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(20,0),(0,8),点D是OA的中点,点P在BC上运动,当△ODP是以10为腰长的等腰三角形时,点P的坐标为(6,8)或(4,8)或(16,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.
A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠ABC=90°且AB=AD | B. | AB=AC且AC⊥BD | C. | AC⊥BD且AC=BD | D. | AC=BD且AB=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数为251mL | B. | 中位数为249mL | C. | 众数为250mL | D. | 方差为$\frac{8}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com