
 如图,AB是⊙O的直径,点D是AB延长线上的一点,DC切⊙O于C,过点A作AE⊥DC(垂足为E)交⊙O于发,CH⊥AB于H,连接HF.
如图,AB是⊙O的直径,点D是AB延长线上的一点,DC切⊙O于C,过点A作AE⊥DC(垂足为E)交⊙O于发,CH⊥AB于H,连接HF.分析 (1)延长CH交圆于G,连接AC,AG,根据垂径定理得到$\widehat{AC}=\widehat{AG}$,求得∠ACH=∠G根据三角形的内角和得到∠EAC+∠ACE=∠ACH+∠CAH=90°,根据弦切角定理得到∠ACE=∠G,等量代换得到∠EAC=∠HAC,根据角平分线的性质即可得到结论;
(2)根据BD=$\frac{1}{3}$AD=3,得到AO=BO=BD=3,求得OD=6,根据切线的性质得到∠OCD=90°,求得∠D=30°,得到∠COD=60°根据切割线定理得到CE2=EF•AE,求得EF=$\frac{C{E}^{2}}{AE}$=$\frac{3}{2}$,得到AF=AE-EF=3,根据余弦定理得即可得到结论.
解答 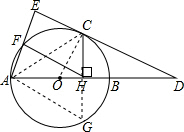 解:(1)延长CH交圆于G,连接AC,AG,
解:(1)延长CH交圆于G,连接AC,AG,
∵AB是⊙O的直径,CH⊥AB于H,
∴$\widehat{AC}=\widehat{AG}$,
∴∠ACH=∠G,
∵AE⊥DC,
∴∠E=90°,
∴∠EAC+∠ACE=∠ACH+∠CAH=90°,
∵DC切⊙O于C,
∴∠ACE=∠G,
∴∠ACE=∠ACH,
∴∠EAC=∠HAC,
∴CE=CH;
(2)∵BD=$\frac{1}{3}$AD=3,
∴AO=BO=BD=3,
∴OD=6,
连接OC,
∵DC切⊙O于C,
∴∠OCD=90°,
∵OC=$\frac{1}{2}$OD,
∴∠D=30°,
∴∠COD=60°,
∵OC=OA,
∴∠OAC=∠OCA=30°,
∴AC=CD=$\sqrt{3}$OC=3$\sqrt{3}$,
∴CE=$\frac{3\sqrt{3}}{2}$,AE=$\frac{9}{2}$,AH=$\frac{1}{2}$AD=$\frac{9}{2}$,
∵DC切⊙O于C,
∴CE2=EF•AE,
∴EF=$\frac{C{E}^{2}}{AE}$=$\frac{3}{2}$,
∴AF=AE-EF=3,
根据余弦定理得:HF2=AF2+AH2-2AF•AHcos60°=32+($\frac{9}{2}$)2-2×$3×\frac{9}{2}$×$\frac{1}{2}$=$\frac{63}{4}$,
∴FH=$\frac{3\sqrt{7}}{2}$.
点评 本题考查了切线的性质,垂径定理,含30°角的直角三角形的性质,余弦定理,正确的作出辅助线是解题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
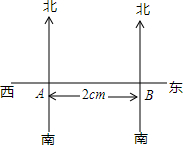 如图,某轮船上午8时在A处测得灯塔S在北偏东60°方向上,当轮船继续向东行驶,中午12时到达B处,在B处测得灯塔S在北偏西30°的方向上,已知轮船行驶的速度为20km/h.
如图,某轮船上午8时在A处测得灯塔S在北偏东60°方向上,当轮船继续向东行驶,中午12时到达B处,在B处测得灯塔S在北偏西30°的方向上,已知轮船行驶的速度为20km/h.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com