
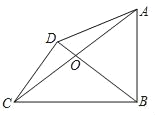
【题目】如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,CD⊥BD,如果CD=3,BC=5,那么AB=_____.
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
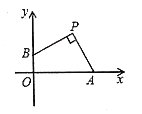
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上运动,且
轴的正半轴上运动,且![]() ,下列结论:
,下列结论:
①![]()
②当![]() 时四边形
时四边形![]() 是正方形
是正方形
③四边形![]() 的面积和周长都是定值
的面积和周长都是定值
④连接![]() ,
,![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
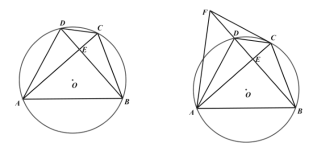
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
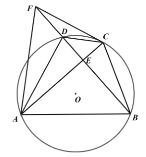
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
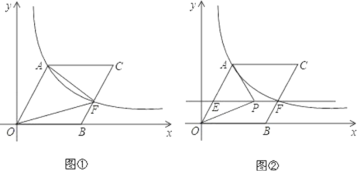
【题目】如图①,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形.![]() .反比例函数
.反比例函数![]() 在第一象限内的图象经过点A,交BC的中点F.且
在第一象限内的图象经过点A,交BC的中点F.且 ![]() .
.
(1)求k值和点C的坐标;
(2)过点F作EF∥OB,交OA于点E(如图②),点P为直线EF上的一个动点,连接PA,PO.是否存在这样的点P,使以P、O、A为顶点的三角形是直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若小明首先选择,则小明选中A品牌单车的概率为 ;
(2)求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )

A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),则称 f(x)是增函数;
(2)若 x1<x2,都有 f(x1)>f(x2),则称 f(x)是减函数.
例题:证明函数f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
证明:设 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数 f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)计算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com