
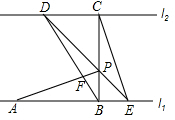
 ��ͼ����ֱ֪��l1��l2���߶�AB��ֱ��l1�ϣ�BC��ֱ��l1��l2�ڵ�C����AB=BC��P���߶�BC���������˵��һ�㣬����P��ֱ�߷ֱ�l2��l1�ڵ�D��E����A��Eλ�ڵ�B�����ࣩ������BP=BE������AP��CE��
��ͼ����ֱ֪��l1��l2���߶�AB��ֱ��l1�ϣ�BC��ֱ��l1��l2�ڵ�C����AB=BC��P���߶�BC���������˵��һ�㣬����P��ֱ�߷ֱ�l2��l1�ڵ�D��E����A��Eλ�ڵ�B�����ࣩ������BP=BE������AP��CE������ ��1������SAS�����ж���ABP�ա�CBE��
��2����֤����ABP�ա�CBD�á�PAB=��DBC���ɡ�PAB+��APB=90��õ���DBC+��APB=90������PFB=90��֤��
��3��ֻҪ֤����FBG�ǵ���ֱ�������μ��ɣ�
��� ��1��֤����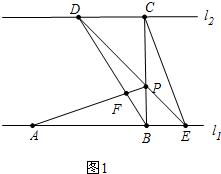 ��ͼ1�У���BC��l1��
��ͼ1�У���BC��l1��
���ABP=��CBE=90�㣬
�ڡ�ABP�͡�CBE�У�
$\left\{\begin{array}{l}{AB=BC}\\{��ABP=��CBE}\\{PB=BE}\end{array}\right.$��
���ABP�ա�CBE��
��2����ͼ2�У���BC=2PB��
��PC=PB=BE��
�ߡ�PBE=90�㣬
���PEB=��BPE=��CPD=45�㣬
��AB��CD��
���ABP+��DCB=180�㣬
���DCP=90�㣬��CDP=45�㣬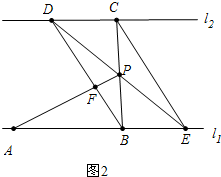
��DC=PC=PB��
�ڡ�ABP�͡�CBD�У�
$\left\{\begin{array}{l}{AB=BC}\\{��ABP=��DCB}\\{PB=CD}\end{array}\right.$��
���ABP�ա�CBD��
���PAB=��DBC��
�ߡ�PAB+��APB=90�㣬
���DBC+��APB=90�㣬
���PFB=90�㣬
��AP��BD��
��3����ͼ3�У�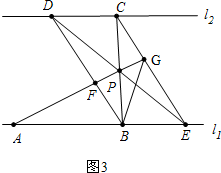 ��RT��PFB��RT��BDC�У�
��RT��PFB��RT��BDC��
��tan��DBC=$\frac{DC}{BC}=\frac{PF}{BF}$=2��
��BF=2PF��
��CD=BE��DC��BE��
���ı���CDBE��ƽ���ı��Σ�
��BD��CE��
���BFP=��CGP��
�ڡ�PBF�͡�PCG�У�
$\left\{\begin{array}{l}{��BPF=��CPG}\\{��BFP=��CGP}\\{PB=PC}\end{array}\right.$��
���PBF�ա�PCG��
��PF=PG��FG=2PF��
��FG=BF��
���AGB=��FBG=45�㣮
���� ���⿼��ȫ�������ε��ж������ʡ�ƽ���ı��ε��ж������ʵ�֪ʶ��Ѱ��������ȫ���ǽ���Ĺؼ��������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
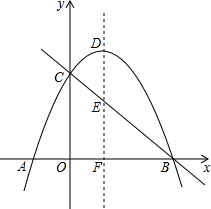 ��ͼ�����κ���y=-$\frac{1}{2}$x2+2x+6��ͼ����x���ཻ��A��B���㣬��y�ύ�ڵ�C������Ϊ��D���ö��κ���ͼ��ĶԳ�����ֱ��BC�ཻ�ڵ�E����x�ύ�ڵ�F��
��ͼ�����κ���y=-$\frac{1}{2}$x2+2x+6��ͼ����x���ཻ��A��B���㣬��y�ύ�ڵ�C������Ϊ��D���ö��κ���ͼ��ĶԳ�����ֱ��BC�ཻ�ڵ�E����x�ύ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
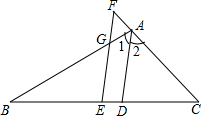 ��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��EΪBC���е㣬����E��EF��AD��AB�ڵ�G����CA���ӳ����ڵ�F����֤��BG=CF��
��ͼ���ڡ�ABC�У�ADƽ�֡�BAC��EΪBC���е㣬����E��EF��AD��AB�ڵ�G����CA���ӳ����ڵ�F����֤��BG=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
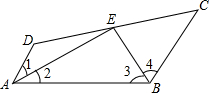 ��ͼ����֪AD��BC����1=��2����3=��4����E��DC�ϣ���˵��AD+BC=AB���������ɣ�
��ͼ����֪AD��BC����1=��2����3=��4����E��DC�ϣ���˵��AD+BC=AB���������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
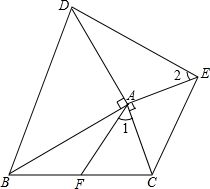 ���������ֱ�����ǰ��ABD����ACE��ͼ�ڷţ�0�㣼��BAC��180�㣬����BC��DE��AF�ǡ�ABC�����ߣ���֤��
���������ֱ�����ǰ��ABD����ACE��ͼ�ڷţ�0�㣼��BAC��180�㣬����BC��DE��AF�ǡ�ABC�����ߣ���֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
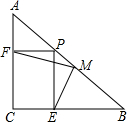 ��֪����ͼ���ڡ�ABC�У�AC=BC����ACB=90�㣬��BA����ȡһ��P��PE��BC��E��PF��AC��F��M��AB���е㣮֤����
��֪����ͼ���ڡ�ABC�У�AC=BC����ACB=90�㣬��BA����ȡһ��P��PE��BC��E��PF��AC��F��M��AB���е㣮֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��1�� | B�� | ��-2��-1�� | ||
| C�� | ��2��-1�� | D�� | ��1��2������-1��2������1��-2������-1��-2�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com