
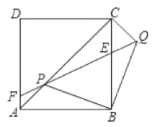
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,P是对角线
中,P是对角线![]() 上的一个动点(点P与A、C不重合),连接
上的一个动点(点P与A、C不重合),连接![]() ,将
,将![]() 绕点B顺时针旋转90°到
绕点B顺时针旋转90°到![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交于点E,
交于点E,![]() 延长线与
延长线与![]() (或
(或![]() 延长线)交于点F.
延长线)交于点F.
(1)连接![]() ,证明:
,证明:![]() ;
;
(2)设![]() ,试写出y关于x的函数关系式,并求当x为何值时,
,试写出y关于x的函数关系式,并求当x为何值时,![]() ;
;
(3)猜想![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
【答案】(1)证明过程见解析;(2)![]() ,当x=3或1时,
,当x=3或1时,![]() ;(3)PF=EQ,证明见解析;
;(3)PF=EQ,证明见解析;
【解析】
(1)证出![]() ,由SAS证明
,由SAS证明![]() 可得结论;
可得结论;
(2)如图证明![]() ,列比利式可得y与x的关系式,根据
,列比利式可得y与x的关系式,根据![]() 计算CE的长,即y的长,代入关系式解方程可得x的值;
计算CE的长,即y的长,代入关系式解方程可得x的值;
(3)如图做辅助线,当F在边AD上时,构建全等三角形,证明![]() ,得EQ=PG,由F、A、G、P四点共圆,得
,得EQ=PG,由F、A、G、P四点共圆,得![]() ,所以△FPG是等腰直角三角形,可得结论;如图,当F在AD延长线上时,同理可得结论.
,所以△FPG是等腰直角三角形,可得结论;如图,当F在AD延长线上时,同理可得结论.
(1)证明:
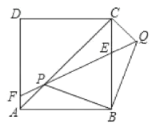
∵线段BP绕点B顺时针旋转![]() 得到线段BQ,
得到线段BQ,
∴BP=BQ,![]() ,
,
∵四边形ABCD是正方形,
∴BA=BC,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
在△BAP和△BCQ中,
∵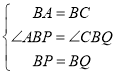 ,
,
∴![]() (SAS),
(SAS),
∴CQ=AP.
(2)如图,

∵四边形ABCD是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵DC=AD=![]() ,
,
由勾股定理可得:
![]() ,
,
∵AP=x,
∴PC=4-x,
∵△PBQ是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ ,
,
由![]() ,
,
∴![]() ,
,
得到![]() ,
,
![]() ,
,
得x=3或x=1.
当x=3或1时,![]() .
.
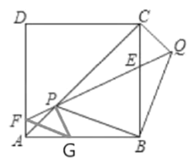
(3)结论:PF=EQ,理由是:
如图,当F在边AD上时,过P作![]() ,交AB于G,则
,交AB于G,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵PB=BQ,![]() ,
,
∴![]() (SAS),
(SAS),
∴EQ=PG,
∵![]() ,
,
∴F、A、G、P四点共圆,
连接FG,
∴![]() ,
,
∴△FPG是等腰直角三角形,
∴PF=PG,
∴PF=EQ.
当F在AD的延长线上时,如图所示,同理可得:PF=PG=EQ.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月22日14时30分,全球新冠肺炎确诊病例达305740例,超过30万,死亡病例累计12762人,将“305740”这个数字用科学记数法表示保留两位有效数字为( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= ![]() 在第一象限内的图象交于点B(
在第一象限内的图象交于点B(![]() ,n).连接OB,若S△AOB=1.
,n).连接OB,若S△AOB=1.
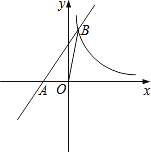
(1)求反比例函数与一次函数的关系式;
(2)直接写出不等式组 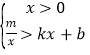 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至E使
至E使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于M,连接
于M,连接![]() ,
,![]() ,H为
,H为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点N、K.则下列结论:
交于点N、K.则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的是______________.(填写所有正确结论的序号)
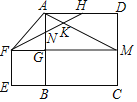
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,∠A=45°,连接BD,且BD⊥AD,点E、点F分别是AB、CD上的点,连接EF交BD于点O,且EF⊥CD,BE=DF=1.
(1)求EF的长;
(2)直接写出ABCD的面积 .

查看答案和解析>>
科目:初中数学 来源: 题型:
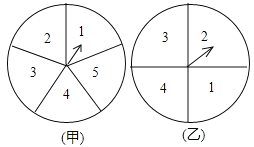
【题目】小明和小亮用如图所示的甲、乙两个转盘(甲转盘被分成五个面积相等的扇形,乙转盘被分成四个面积相等的扇形)做游戏,转动两个转盘各一次(如果指针恰好在分割线上,那么重转一次,直到指针指向某一扇形区域为止).
(1)请你求出甲转盘指针指向偶数区域的概率;
(2)若两次数字之和为![]() ,
,![]() 或
或![]() 时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
时,则小明胜,否则小亮胜,这个游戏对双方公平吗?请你用树状图或列表法说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
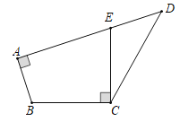
【题目】(1)如图,一块四边形纸板剪去![]() ,得到四边形
,得到四边形![]() ,测得
,测得![]() ,
,![]() ,
,![]() .能否在四边形纸板
.能否在四边形纸板![]() 上只剪一刀,使剪下的三角形与
上只剪一刀,使剪下的三角形与![]() 全等?请说明理由.
全等?请说明理由.
(2)我市某学校八年级同学乘坐大巴车去长江青少年素质教育实践基地参加综合实践活动.1号车出发4分钟后,2号车才出发,结果两车同时到达.已知素质教育基地距离该校18千米,2号车的平均速度是1车的平均速度的![]() 倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
倍.请你就“1号车”提出一个用分式方程解决的问题,并写出解题过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com