Question

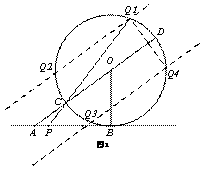
已知AB是圆O的切线，切点为B，直线AO交圆O于C、D两点，CD＝2，∠DAB=30°,动点P在直线AB上运动，PC交圆O于另一点Q，

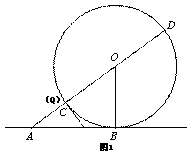
（1）当点P，运动到Q、C两点重合时（如图1），求AP的长。

（2）点运动过程中，有几个位置（几种情况）使△CQD的面积为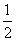?（　直接写出答案）

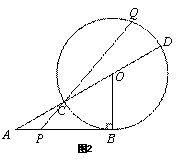
（3）当使△CQD的面积为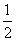，且Q位于以CD为直径的的上半圆上，CQ＞QD时（如图2），求AP的长。

 

 

Answer 1

解：∵AB是圆O的切线

∴∠OBA＝90°

∵ABC中，CD＝2，∠DAB=30°

∴OB＝1

∴OB＝OC＝AC＝1

∵当点P，运动到Q、C两点重合时

∴PC为圆O的切线

∴∠PCA＝90°

∵∠DAB=30°，AC＝1

∴AP＝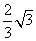

（2）利用三角形的面积公式，知底和积可求高，然后用平行线去截圆，即可以得到解。

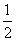由于CD的长度2，而S△CQD＝，故CD上的高的长度为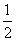：，从而如图，我们可得到答案：

（3）利用S△CQD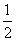＝，求出CD上的高QN的长度，过点PM⊥AD于点M，

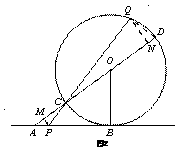然后利用相似△QCN∽△DQN求出CN的长度，再次利用相似△PMC∽△QNC，从而得到MC与MP的关系，由已知易知AM＝，由AC＝1，从而可以解出MP，从而求出AP的长度。