
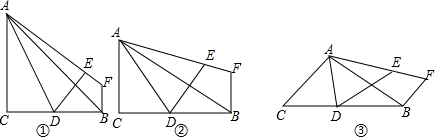
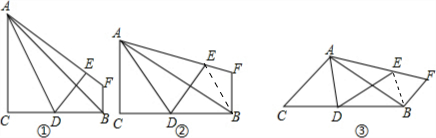
 解:(1)观察图形,可以发现BF=EF.故答案为:相等.
解:(1)观察图形,可以发现BF=EF.故答案为:相等.

 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
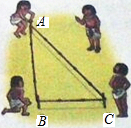 相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.
相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
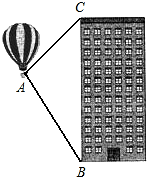 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
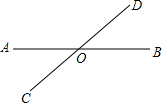 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.查看答案和解析>>
科目:初中数学 来源: 题型:
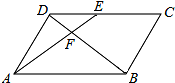 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com