
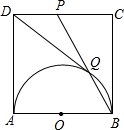
 如图,在正方形ABCD中,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ.给出如下结论:
如图,在正方形ABCD中,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ.给出如下结论:分析 ①连接OD,OQ,证明△AOD与△QOD全等即可;
②连接AQ,借助三角函数和勾股定理求出PQ,BQ的长度即可求解;
③连接AQ,OQ,借助①②的相关结论,结合三角形外角的性质和同角的余角(补角)相等即可求解;
④过点Q作QH⊥CD,求出三角形DQH的三边长度即可确定相关的三角函数.
解答 解:①如图1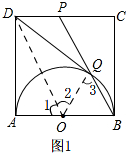
连接DO,OQ,在正方形ABCD中,AB∥CD,AB═CD,
∵P是CD中点,O是AB中点,
∴DP∥OB,DP═OB,
∴四边形OBDP是平行四边形,
∴OD∥BP,
∴∠1=∠OBQ,∠2=∠3,
又∵OQ=OB,
∴∠3=∠OBQ,
∴∠1=∠2,
在△AOD和△QOD中,
$\left\{\begin{array}{l}{AO=QO}\\{∠1=∠2}\\{OD=OD}\end{array}\right.$,
∴△AOD≌△QOD,
∴∠OQD=∠A=90°,
∴DQ与半圆O相切,
①正确;
②如图2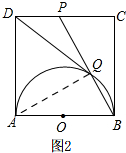
连接AQ,可得:∠AQB=90°,
在正方形ABCD中,AB∥CD,
∴∠ABQ=∠BPC,
设正方形边长为x,则CP=$\frac{1}{2}$x,
由勾股定理可求:BP=$\frac{\sqrt{5}}{2}$,
∴cos∠BPC=$\frac{\sqrt{5}}{5}$,cos∠ABQ=$\frac{\sqrt{5}}{5}$,
∴$\frac{BQ}{AB}$=$\frac{\sqrt{5}}{5}$,又AB=x,
可求,BQ=$\frac{\sqrt{5}}{5}$x,
PQ=$\frac{3\sqrt{5}}{10}$x,
∴$\frac{PQ}{BQ}$=$\frac{3}{2}$,
②不对;
③如图3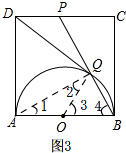
连接AQ,OQ,
由①知,∠OQD=90°,又∠OAD=90°,可求∠ADQ+∠AOQ=180°,
∵∠3+∠AOQ=180°,
∴∠3=∠ADQ,
由②知,∠1+∠4=90°,
又∠4+∠CBP=90°,
∴∠CBP=∠1,
∵OA=OQ,
∴∠1=∠2,
又∵∠3=∠1+∠2,
∴∠3=2∠CBP,
∴∠ADQ=2∠CBP,
故③正确;
④如图4,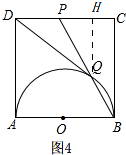
过点Q作QH⊥CD,
易证QH∥BC,
设正方形边长为x,由②知:PQ=$\frac{3\sqrt{5}}{10}$x,cos∠BPC=$\frac{\sqrt{5}}{5}$,
可求:PH=$\frac{3}{10}$x,HQ=$\frac{3}{5}$x,
∴DH=DP+PH=$\frac{4}{5}$x,
由勾股定理可求:DQ=x,
∴cos∠CDQ=$\frac{DH}{DQ}$=$\frac{4}{5}$,
故④不正确.
综上所述:正确的有①③.
点评 此题考查圆的综合问题,熟悉正方形的性质,会构造平行四边形并运用其性质,会结合圆的性质构造直角三角形,构造全等三角形,会证明切线,能熟练的运用三角函数是解题的关键.


科目:初中数学 来源: 题型:解答题
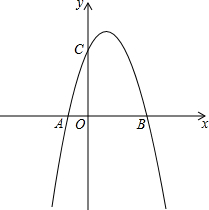 如图所示,抛物线y=ax2+bx+3与x轴交于点A、B两点(A在B的左侧)与y轴交于C点,且OA:OC=1:3,S△ABC=6.
如图所示,抛物线y=ax2+bx+3与x轴交于点A、B两点(A在B的左侧)与y轴交于C点,且OA:OC=1:3,S△ABC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com