
分析 (1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(4)方程去括号,移项合并,把x系数化为1,即可求出解;
(5)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)原式=-4×(-$\frac{1}{2}$)+8÷4=2+2=4;
(2)原式=($\frac{12}{7}$+6+3-$\frac{1}{2}$)×(-$\frac{1}{3}$)=-$\frac{4}{7}$-3+$\frac{1}{6}$=-3$\frac{17}{42}$;
(3)原式=-1+9-72=-64;
(4)去括号得:4x+6x-15=7-x,
移项合并得:11x=22,
解得:x=2;
(5)方程整理得:5x+20-2x+6=-1.3,
移项合并得:3x=-27.3,
解得:x=-9.1;
(6)去分母得:6(x+4)-30x+150-10(x+3)=-15(x-2),
去括号得:6x+24-30x+150-10x-30=-15x+30,
移项合并得:-19x=-114,
解得:x=6.
点评 此题考查了有理数的混合运算,以及解一元一次方程,熟练掌握运算法则是解本题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:填空题
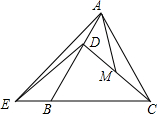 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
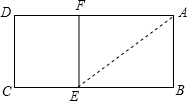 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有两个不同型号的手机(分别记为A、B)和与之匹配的保护盖(分别记为a、b)(如图所示),散乱地放在桌子上,若从这四个物件中随机取两个,求恰好匹配的概率.
有两个不同型号的手机(分别记为A、B)和与之匹配的保护盖(分别记为a、b)(如图所示),散乱地放在桌子上,若从这四个物件中随机取两个,求恰好匹配的概率.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
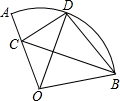 如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π.
如图,在扇形AOB中,∠AOB=100°,半径OA=9,将扇形OAB沿着过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长等于2π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com