
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积为( )| A. | a-b | B. | a+b | C. | ab | D. | a2-ab |
分析 设大正方形的边长为x1,小正方形的边长为x2,根据图示可得等量关系:①大正方形边长+2个小正方形的边长=a,②大正方形边长-2个小正方形的边长=b,解出x1、x2的解,再利用大正方形的面积减去4个小正方形的面积即可求解.
解答 解:设大正方形的边长为x1,小正方形的边长为x2,由图①和②列出方程组得,
$\left\{\begin{array}{l}{{x}_{1}+2{x}_{2}=a}\\{{x}_{1}-2{x}_{2}=b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{a+b}{2}}\\{{x}_{2}=\frac{a-b}{4}}\end{array}\right.$;
②的大正方形中未被小正方形覆盖部分的面积=($\frac{a+b}{2}$)2-4×($\frac{a-b}{4}$)2=ab.
故选:C.
点评 本题考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的关系,表示出大小两个正方形的边长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1≤k≤1 | B. | 0<k≤1 | C. | k≤1 | D. | k≤-1或k≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
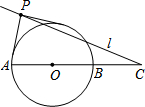 如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.
如图,已知⊙O的半径为2,C为直径AB延长线上一点,BC=2.过C任作一直线l.若l上总存在点P,使过P所作的⊙O的两切线互相垂直,则∠ACP的最大值等于45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
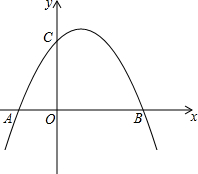 如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.
如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB.
如图,已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC,交⊙O于点D,交AC于点E,连接BD,BD交AC于点F,延长AC到点P,连接PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com