
| 1 |
| 1��2 |
| 1 |
| 2 |
| 1 |
| 2��3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3��4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 1��2 |
| 1 |
| 2��3 |
| 1 |
| 3��4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| 1��2 |
| 1 |
| 2��3 |
| 1 |
| 3��4 |
| 1 |
| 2006��2007 |
| 1 |
| 2��4 |
| 1 |
| 4��6 |
| 1 |
| 6��8 |
| 1 |
| 2006��2008 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2006 |
| 1 |
| 2007 |
| 1 |
| 2007 |
| 2006 |
| 2007 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2006 |
| 1 |
| 2008 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2008 |
| 1003 |
| 4016 |
| 1 |
| n |
| 1 |
| n+1 |
| 2006 |
| 2007 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
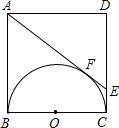 ��ͼ��������ABCD�߳�Ϊ4cm���������ε�һ��BCΪֱ����������ABCD������Բ���ٹ�A����Բ�����ߣ����Բ������F�㣬��DC�ཻ��E�㣬���ADE�����Ϊ
��ͼ��������ABCD�߳�Ϊ4cm���������ε�һ��BCΪֱ����������ABCD������Բ���ٹ�A����Բ�����ߣ����Բ������F�㣬��DC�ཻ��E�㣬���ADE�����Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 8 |
| 3 |
| 3 |
| 8 |
| 1 |
| 2 |
| 5 |
| 6 |
| 8 |
| 9 |
| 1 |
| 2 |
| 1 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 6 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��4��5��10 |
| B��3��4��5 |
| C��1��3��4 |
| D��1��2��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2-4x+4 |
| 9+6x+x2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 | ||
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
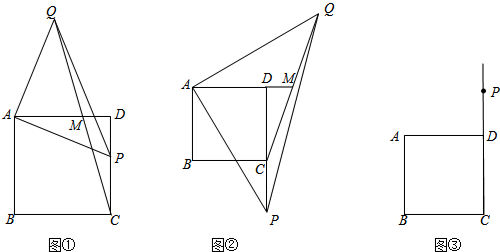
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com