

分析 (1)利用一副直角三角板的特点得出∠BDC=∠BCD,进而得出∠DOC=∠BDC,即可求出答案;
(2)首先作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,再利用直角三角形的性质求出BC,BD的长,即可得出AD的长.
解答  (1)证明:如图1所示:∵BC=DE,
(1)证明:如图1所示:∵BC=DE,
∴∠BDC=∠BCD,
∵∠DEF=30°,
∴∠BDC=∠BCD=75°,
∵∠ACB=45°,
∴∠DOC=30°+45°=75°,
∴∠DOC=∠BDC,
∴△CDO是等腰三角形;
(2)解:作AG⊥BC,垂足为点G,DH⊥BF,垂足为点H,
在Rt△DHF中,∵∠F=60°,DF=10,
∴DH=5$\sqrt{3}$,HF=5,
在Rt△BDF中,∵∠F=60°,DF=10,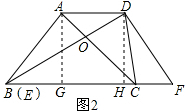
∴DB=10$\sqrt{3}$,BF=20,
∴BC=BD=10$\sqrt{3}$,
∵AG⊥BC,∠ABC=45°,
∴BG=AG=5$\sqrt{3}$,
∴AG=DH,
∵AG∥DH,
∴四边形AGHD为矩形,
∴AD=GH=BF-BG-HF=20-5$\sqrt{3}$-5=15-5$\sqrt{3}$.
点评 此题主要考查了勾股定理以及直角三角形的性质、等腰三角形的判定等知识,正确得出BG=AG的长是解题关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
 2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;
2015年全球葵花籽产量约为4200万吨,比2014年上涨2.1%,某企业加工并销售葵花籽,假设销售量与加工量相等,在图中,线段AB、折线CDB分别表示葵花籽每千克的加工成本y1(元)、销售价y2(元)与产量x(kg)之间的函数关系;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$)2=9 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-8}$=2 | D. | $\sqrt{36}$=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
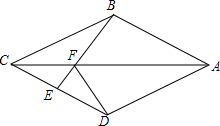 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2+5 | B. | y=(x-2)2-l | C. | y=(x-2)2-3 | D. | y=x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
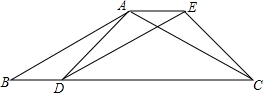 如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.
如图,已知四边形ABDE是平行四边形,C为边BD延长线上一点,连结AC、CE,使AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com