Question

【背景知识】
数轴是初中数学的一个重要工具．利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上A点、B点表示的数为a、b，则A，B两点之间的距离AB=|a-b|，若a＞b，则可简化为AB=a-b；线段AB的中点M表示的数为

a+b

2

．
【问题情境】
已知数轴上有A、B两点，分别表示的数为-10，8，点A以每秒3个单位的速度沿数轴向右匀速运动，点B以每秒2个单位向左匀速运动．设运动时间为t秒（t＞0）．

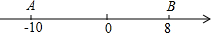
【综合运用】
（1）运动开始前，A、B两点的距离为

 

；线段AB的中点M所表示的数

 

．
（2）点A运动t秒后所在位置的点表示的数为

 

；点B运动t秒后所在位置的点表示的数为

 

；（用含t的代数式表示）
（3）它们按上述方式运动，A、B两点经过多少秒会相遇，相遇点所表示的数是什么？
（4）若A，B按上述方式继续运动下去，线段AB的中点M能否与原点重合？若能，求出运动时间，并直接写出中点M的运动方向和运动速度；若不能，请说明理由．（当A，B两点重合，则中点M也与A，B两点重合）

Answer 1

考点：一元一次方程的应用,数轴,两点间的距离

专题：

分析：（1）根据A，B两点之间的距离AB=|a-b|，若a＞b，则可简化为AB=a-b及线段AB的中点M表示的数为

a+b

2

即可求解；
（2）点A运动t秒后所在位置的点表示的数=运动开始前A点表示的数+点A运动的路程，点B运动t秒后所在位置的点表示的数=运动开始前B点表示的数-点B运动的路程；
（3）设它们按上述方式运动，A、B两点经过x秒会相遇，等量关系为：点A运动的路程+点B运动的路程=18，依此列出方程，解方程即可；
（4）设A，B按上述方式继续运动t秒线段AB的中点M能否与原点重合，根据线段AB的中点表示的数为0列出方程，解方程即可．

解答：解：（1）运动开始前，A、B两点的距离为8-（-10）=18；线段AB的中点M所表示的数为

-10+8

2

=-1；

（2）点A运动t秒后所在位置的点表示的数为-10+3t；点B运动t秒后所在位置的点表示的数为8-2t；

（3）设它们按上述方式运动，A、B两点经过x秒会相遇，根据题意得
-10+3x=8-2x，
解得 x=

18

5

，
-10+3x=

4

5

．
答：A、B两点经过

18

5

秒会相遇，相遇点所表示的数是

4

5

；

（4）由题意得，

(-10+3t)+(8-2t)

2

=0，
解得 t=2，
答：经过2秒A，B两点的中点M会与原点重合．M点的运动方向向右，运动速度为每秒

1

2

个单位长度．
故答案为18，-1；-10+3t，8-2t．

点评：本题考查了一元一次方程的应用应用和数轴，解题的关键是掌握点的移动与点所表示的数之间的关系，根据题目给出的条件，找出合适的等量关系列出方程，再求解．