练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

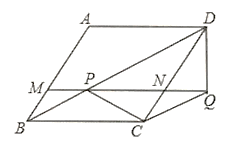
    【题目】在菱形中，，点是对角线上一动点，将线段绕点顺时针旋转120°到，连接，连接并延长，分别交于点．

    （1）求证：；

    （2）已知，若的最小值为，求菱形的面积．

    【答案】（1）证明见解析；（2）菱形的面积．

    【解析】

    （1）利用SAS证明；

    （2）先求出，得到，故当时，最小，此时最小，根据MN=，求出PC=2，BC=2PC=4，再利用菱形的面积得到答案.

    （1）证明：四边形是菱形，且，

    ∴，

    ∴，

    由旋转的性质得：

    ∴，

    ∴；

    （2）连接AC，

    ∵四边形ABCD是菱形，

    ∴AB=BC，

    ∵，

    ∴△ABC是等边三角形，

    ∴AB=BC,

    ∵，

    ∴，

    ∴，

    ∴当时，最小，此时最小，

    ∵MN=，

    ∴PC=2，

    ∵∠DBC=，∠BPC=90°，

    ∴BC=2PC=4，

    ∴菱形的面积

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

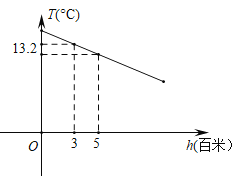
    【题目】某地区山峰的高度每增加1百米，气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题：

    （1）求高度为5百米时的气温．

    （2）求T关于h的函数表达式．

    （3）测得山顶的气温为6℃，求该山峰的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

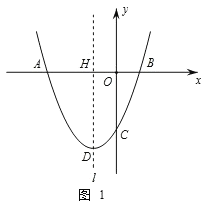
    【题目】如图1，已知抛物线经过A(－3，0)，B(1，0)，C(0，－3)三点，其顶点为D，对称轴是直线，与x轴交于点H．

    （1）求该抛物线的解析式；

    （2）若点P是该抛物线对称轴上的一个动点，求△PBC周长的最小值；

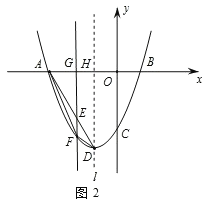
    （3）如图2，若E是线段AD上的一个动点（E与A、D不重合），过E点作平行于y轴的直线交抛物线于点F，交x轴于点G，设点E的横坐标为m，△ADF的面积为S．

    ①试求S与m的函数关系式；

    ②S是否存在最大值？若存在，求出最大值及此时点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个运输小队分别从两个仓库以相同的工作效率调运一批物资，两队同时开始工作．第二小队工作5天后，由于技术问题检修设备5天，为赶上进度，再次开工后他们将工作效率提高到原先的2倍，结果和第一小队同时完成任务．在两队调运物资的过程中，两个仓库物资的剩余量y t与第一小队工作时间x天的函数图像如图所示．

    （1）①求线段AC所表示的y与x之间的函数表达式；

    ②求点F的坐标，并解释点F的实际意义．

    （2）如果第二小队没有检修设备，按原来的工作效率正常工作，那么他们完成任务的天数是 天．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为缓解某学校大班额现状，某市决定通过新建学校来解决该问题．经测算，建设6个小学，5个中学，需费用13800万元，建设10个小学，7个中学，需花费20600万元．

    （1）求建设一个小学，一个中学各需多少费用．

    （2）该市共计划建设中小学80所，其中小学的建设数量不超过中学建设数量的1.5倍．设建设小学的数量为x个，建设中小学校的总费用为y万元．

    ①求y关于x的函数关系式；

    ②如何安排中小学的建设数量，才能使建设总费用最低？

    （3）受国家开放二胎政策及外来务工子女就读的影响，预计在小学就读人数会有明显增加，现决定在（2）中所定的方案上增加投资以扩大小学的就读规模，若建设小学总费用不超过建设中学的总费用，则每所小学最多可增加多少费用？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两个芭蕾舞团演员的身高（单位：cm）如下表：

    两组芭蕾舞团演员身高的方差较小的是______．（填“甲”或“乙”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系中的点P和图形M，给出如下定义：Q为图形M上任意一点，如果两点间的距离有最大值，那么称这个最大值为点P与图形M间的开距离，记作．已知直线与x轴交于点A，与y轴交于点B，的半径为1．

    （1）若，

    ①求的值；

    ②若点C在直线上，求的最小值；

    （2）以点A为中心，将线段顺时针旋转得到，点E在线段组成的图形上，若对于任意点E，总有，直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转一定的角度α得到△DEC，点A、B的对应点分别是D、E．

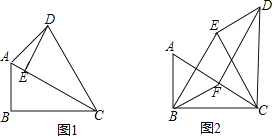
    （1）当点E恰好在AC上时，如图1，求∠ADE的大小；

    （2）若α＝60°时，点F是边AC中点，如图2，求证：四边形BEDF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

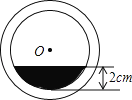
    【题目】将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒，水平放置在桌面上，水杯的底面如图所示，已知水杯内径（图中小圆的直径）是8cm，水的最大深度是2cm，则杯底有水部分的面积是（　　）

    A.（π﹣4）cm2B.（π﹣8）cm2

    C.（π﹣4）cm2D.（π﹣2）cm2

    查看答案和解析>>

    同步练习册答案