练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．已知梯形ABCD中，AD∥BC，则∠A：∠B：∠C：∠D不可能是（　　）
    A．3：7：5：5B．5：4：5：4C．4：5：6：3D．8：1：4：5

    分析 由梯形的性质得出同旁内角互补，得出A、C、D有可能；由平行四边形的判定方法得出B不可能．

    解答 解：∵AD∥BC，
    ∴∠A+∠B=180°，∠C+∠D=180°，
    即∠A+∠B=∠C+∠D，
    ∴A、C、D选项有可能；
    B选项不可能；
    ∵若∠A：∠B：∠C：∠D=5：4：5：4，
    则∠A=∠C，∠B=∠D，
    则四边形ABCD是平行四边形，
    ∴B不可能．
    故选：B．

    点评 本题考查了梯形的性质、平行四边形的判定方法；熟练掌握梯形的性质，并能进行推理论证是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

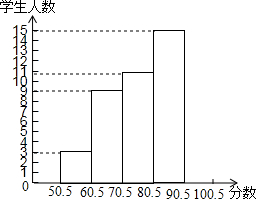    9．为了了解奥运知识，某中学举行了一次“奥运知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分），进行统计，请你根据下面尚未完成的统计表和统计图，解答下列问题．
     分组 频数 频率
     50.5～60.5 3 0.06
    60.5～70.5 9 A
     70.5～80.5 11 0.22
     80.5～90.5 15 0.30
     90.5～100.5 B C
    （1）根据以上信息，统计表中A=0.18，B=12，C=0.24；
    （2）补全统计图；
    （3）在该问题中，个体是每一个学生的竞赛成绩；
    （4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，在矩形ABCD中，以B为圆心，BC长为半径作弧，交AD于E，连接BE，过C点作CF⊥BE于F．
    求证：BF=AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

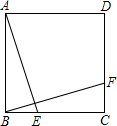    7．如图，E，F分别是正方形ABCD的边BC，CD上的点，且BE=CF，连接AE，BF，将△ABE绕正方形的中心按逆时针方向旋转α（0＜α＜180°）到∠BCF，则旋转角α等于（　　）
    A．90°B．60°C．45°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

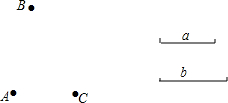    14．如图，已知平面上三个点A，B，C和线段a，b，按下列要求画图．
    （1）画AB，画射线AC，画直线BC；
    （2）在线段AB上作线段AM=a，在线段AC的延长线上作线段CN=b，连接MN交直线BC于点D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

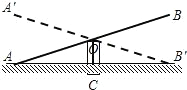    4．如图，是跷跷板的示意图，支柱OC与地面垂直，O是AB的中点，若∠OAC=20°，当跷跷板绕O转到A′B′位置时，∠AOA′的大小是（　　）
    A．40°B．60°C．80°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，已知△ACD∽△BCA，若CD=4，AC=6，则BC等于（　　）
    A．9B．10C．11D．12

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．观察下列4个命题：
    （1）三角形的外角和是180°；       
    （2）三角形的三个内角中至少有两个锐角；
    （3）如果x2y＜0，那么y＜0；         
    （4）（x-$\frac{1}{2}$）2=x2-$\frac{1}{4}$x+1．
    其中真命题是（　　）
    A．（1）（2）B．（2）（3）C．（2）（4）D．（3）（4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．己知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长，则这个直角三角形的斜边上的高为（　　）
    A．12B．6C．5D．$\frac{12}{5}$

    查看答案和解析>>

    同步练习册答案