
【题目】如图,在Rt△ABC中,∠ACB=90°,BC,AC,AB边的中点分别是点D,E,F,则下列说法可能不正确的为( )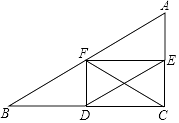
A.四边形CDFE是矩形
B.DE=CF= ![]() AB
AB
C.S△ABC=4S△AEF
D.∠B=30°
【答案】D
【解析】解:∵点D,E,F分别是BC,AC,AB的中点,
∴DF∥AC,EF∥BC,
∴四边形CDFE是平行四边形,
∵∠ACB=90°,
∴平行四边形CDFE是矩形,故A正确,
∴CF=DE,
∵点D,E是BC,AC中点,
∴DE= ![]() AB,
AB,
∴DE=CF= ![]() AB,
AB,
故B正确,
∵点E,F是AC,AB的中点,
∴EF= ![]() BC,EF∥BC,
BC,EF∥BC,
∴△AEF∽△ACB,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△ABC=4S△AEF,
故C正确,
所以,A,B,C都正确,
即:不正确的只有D,
所以答案是:D.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
则m与v之间的关系最接近于下列各关系式中的( )
A. v=2m-1B. v=m2-1C. v=3m-3D. v=m+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小区的一个健身器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端点A到地面CD的距离(精确到0.1m).(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
车型 | 目的地 | ||
A村(元/辆) | B村(元/辆) | ||
大货车 | |||
800 | 900 | ||
小货车 | 400 | 600 | |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用水,某市自来水公司对居民用水采用以户为单位分段计费办法收费,即一个月用水10t以内(包含10t)的用户,收水费a元/t,一月用水超过10t的用户,超出的部分按b元/t(b>a)收费,设一户居民用水x t,应收水费y元,y与x之间的函数关系式如图所示:按上述分段收费标准,小兰家3月份和4月份分别交水费29.1元和20.8元,则小兰家4月份比3月份节约用水吨.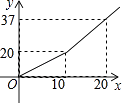
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.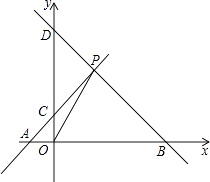
(1)求△AOP的面积;
(2)若S△BOP=3S△AOP , 求直线BD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E是AD的中点,如果OE=2,AD=6,那么ABCD的周长是( )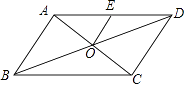
A.20
B.12
C.24
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面上四点A(0,0),B(10,0),C(12,6),D(2,6),直线y=mx﹣3m+6将四边形ABCD分成面积相等的两部分,则m的值为( )
A.![]()
B.﹣1
C.2
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com