
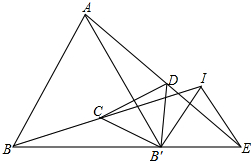
 如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.
如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.
|
|


科目:初中数学 来源: 题型:
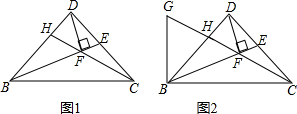
| DH |
| BH |
查看答案和解析>>
科目:初中数学 来源: 题型:
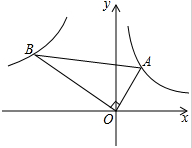 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=| 1 |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 |
| 3 |
| 5 |
| 3 |
| A、∠B=∠A′ |
| B、∠A=∠C′ |
| C、∠A>∠B′ |
| D、∠C=∠B′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
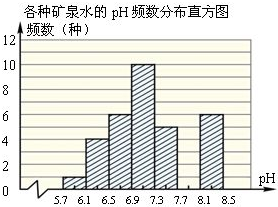 2008年 5月12日,我国四川省发生里氏8.0级地震,社会各界纷纷伸出援助之手捐钱捐物.根据国家质检总局的通知要求,对送往灾区食品、重要消费品必须进行检验检测,以确保运往灾区的食品等救灾物资的质量安全.如图是对某批数种矿泉水的抽查统计图,请观察图形,并回答下列问题:
2008年 5月12日,我国四川省发生里氏8.0级地震,社会各界纷纷伸出援助之手捐钱捐物.根据国家质检总局的通知要求,对送往灾区食品、重要消费品必须进行检验检测,以确保运往灾区的食品等救灾物资的质量安全.如图是对某批数种矿泉水的抽查统计图,请观察图形,并回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com