练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，中，，，，是线段上一个动点，以为边在外作等边．若是的中点，则的最小值为（ ）

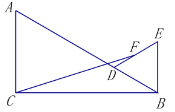
    A.6B.8C.9D.10

    【答案】C

    【解析】

    过点D作DG⊥BC于G，过点F作FH⊥BC于H，设等边△BDE的边长为x，解直角三角形BG，DG，再求出∠CBE=90°，然后根据梯形的中位线等于两底和的一半求出FH，再求出CH，然后利用勾股定理列式表示出CF2，再根据二次函数的增减性求出CF2的最小值，然后开方即可．

    解：如图，过点D作DG⊥BC于G，过点F作FH⊥BC于H，

    设等边△BDE的边长为x，

    ∵∠ABC=30°，

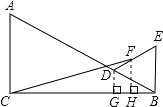
    ∴BG=x，DG=x，

    ∵∠ABC=30°，△BDE是等边三角形，

    ∴∠CBE=90°，

    ∵F为DE中点，

    ∴FH是梯形BEDG的中位线，

    在中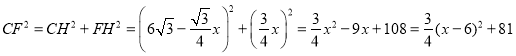

    为线段AB上一个动点

    当时 有最小值81

    :CF的最小值为，

    故选择：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示的正方形网格中，△的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：

    （1）作出△关于y轴对称的△ A1B1C1，并写出点C1的坐标．

    （2）以点为旋转中心，将△绕点顺时针旋转得△ A2B2C2，画出△ A2B2C2 ，并写出点C2的坐标．

    （3）画出△关于坐标原点成中心对称的△ A3B3C3，并写出点C3的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图像与x轴交于点(-2，0)、()，且，与y轴的正半轴的交点在(0，2)的下方，则下列结论中：①ab>0；②4a-2b+c=0；③2a-b+1<0；④a<b<c，其中正确的结论有( ).

    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

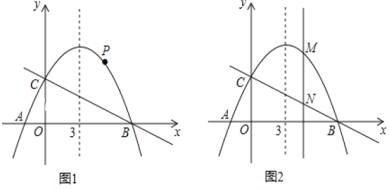
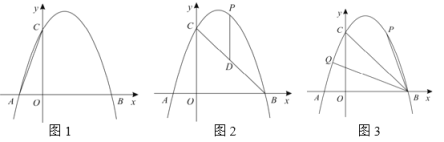
    【题目】如图， 已知抛物线的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点 ．

    （1）求抛物线的解析式和A、B两点的坐标；

    （2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；

    （3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

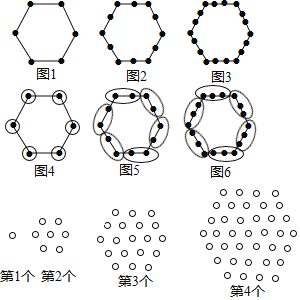
    【题目】“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．

    例如：图1有6个点，图2有12个点，图3有18个点，……，按此规律，求图10、图n有多少个点？

    我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是6×1=6个；图2中黑点个数是6×2=12个：图3中黑点个数是6×3=18个；所以容易求出图10、图n中黑点的个数分别是　 　、　 　．

    请你参考以上“分块计数法”，先将下面的点阵进行分块（画在答题卡上），再完成以下问题：

    （1）第5个点阵中有　 　个圆圈；第n个点阵中有　 　个圆圈．

    （2）小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线过点轴上的和点，交轴于点，点该物上限一点，且．

    （1）抛物线的解析式为：____________；

    （2）如图2，过点作轴交直线于点，求点在运动的过程中线段长度的最大值；

    （3）如图3，若，在对称轴左侧的抛物线上是否存在点，使？若存在，请求出点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某生产商存有1200千克产品，生产成本为150元/千克，售价为400元千克.因市场变化，准备低价一次性处理掉部分存货，所得货款全部用来生产产品，产品售价为200元/千克.经市场调研发现，产品存货的处理价格（元/千克）与处理数量（千克）满足一次函数关系（），且得到表中数据.

    （千克）

    （元/千克）

    200

    350

    400

    300

    （1）请求出处理价格（元千克）与处理数量（千克）之间的函数关系；

    （2）若产品生产成本为100元千克，产品处理数量为多少千克时，生产产品数量最多，最多是多少？

    （3）由于改进技术，产品的生产成本降低到了元/千克，设全部产品全部售出，所得总利润为（元），若时，满足随的增大而减小，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个不透明的布袋里装有16个只有颜色不同的球，其中红球有x个，白球有2x个，其他均为黄球，现甲从布袋中随机摸出一个球，若是红球则甲同学获胜，甲同学把摸出的球放回并搅匀，由乙同学随机摸出一个球，若为黄球，则乙同学获胜。

    （1）当X=3时，谁获胜的可能性大？

    （2）当x为何值时，游戏对双方是公平的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知点G在正方形ABCD的对角线AC上，GE⊥BC，垂足为点E，GF⊥CD，垂足为点F．

    （1）证明与推断：

    ①求证：四边形CEGF是正方形；

    ②推断：的值为　 　：

    （2）探究与证明：

    将正方形CEGF绕点C顺时针方向旋转α角（0°＜α＜45°），如图（2）所示，试探究线段AG与BE之间的数量关系，并说明理由：

    （3）拓展与运用：

    正方形CEGF在旋转过程中，当B，E，F三点在一条直线上时，如图（3）所示，延长CG交AD于点H．若AG=6，GH=2，则BC=　 　．

    查看答案和解析>>

    同步练习册答案