
����Ŀ����ͼ����һ��ƽ���ı���ֽƬABCD�У���һ�����Σ��ס�����λͬѧ�Ļ������£��ף���B��AΪԲ�ģ�AB��Ϊ�뾶�������ֱ�BC��AD�ڵ�E��F�����ı���ABEFΪ���Σ��ң�����A����B��ƽ����AE��BF���ֱ�BC�ڵ�E����AD�ڵ�F�����ı���ABEF�����Σ����ڼס������˵Ļ����������ж���ȷ���ǣ�������
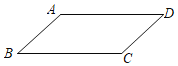
A. ������ȷB. ������ȷ
C. �ס��Ҿ���ȷD. �ס��Ҿ�����
���𰸡�C
��������
���ݻ�����ͼ�Լ����ε��ж���֪���Ҷ�����ȷ�ģ�
�⣺��������ȷ����AF=AB��BE=AB
��AF=BE��
��ABCD��AD��BC��
��AF��BE��
���ı���ABEFΪƽ���ı��Σ�
��AF=AB��
���ı���ABEFΪ���Σ��ڱ���ȵ�ƽ���ı��������Σ���
�ҵ�������ȷ��
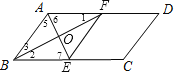
��AD��BC��
���1=��2����6=��7��
��BFƽ����ABC��AEƽ����BAD��
���2=��3����5=��6��
���1=��3����5=��7��
��AB=AF��AB=BE��
��AF=BE
��AF��BE����AF=BE��
���ı���ABEF��ƽ���ı��Σ�
��AB=AF��
��ƽ���ı���ABEF�����Σ�
��ѡ��C��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����һ����ֽƬABCD����EF�۵���CE��AF�ڵ�G������G��GH��EF�����߶�BE�ڵ�H��

���ж�EG��EH�Ƿ���ȣ���˵�����ɣ�
���ж�GH�Ƿ�ƽ�֡�AGE����˵�����ɣ�
��2����ͼ2���������1���е���֪������Ϊ�۵�������ֽƬABC�������������䣮
���ж�EG��EH�Ƿ���ȣ���˵�����ɣ�
���ж�GH�Ƿ�ƽ�֡�AGE�����ƽ�֣���˵�����ɣ������ƽ�֣����õ�ʽ��ʾ��EGH����AGH���C��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AB=20��BC=15��CD=7��AD=24����B=90����
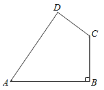
��1���жϡ�D�Ƿ���ֱ�ǣ���˵�����ɣ�
��2�����ı���ABCD�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺�� ![]() Ϊ���������㣬����
Ϊ���������㣬����![]() ��
��![]() �ľ����ǵ�
�ľ����ǵ�![]() ��
��![]() �ľ���
�ľ���![]() �������ǾͳƵ�
�������ǾͳƵ�![]() ��
��![]() ���ɵ�.��
���ɵ�.�� ![]() Ϊ���������㣬����
Ϊ���������㣬����![]() ��
��![]() �ľ����ǵ�
�ľ����ǵ�![]() ��
�� ![]() �ľ���һ�룬���ǾͳƵ�
�ľ���һ�룬���ǾͳƵ�![]() ��
��![]() �����.��ͼ����
�����.��ͼ����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����ʾ
����ʾ![]() �ĵ�
�ĵ�![]() ����
����![]() �ľ�����
�ľ�����![]() ������
������![]() �ľ�����
�ľ�����![]() ����ô��
����ô��![]() ��
��![]() ���ɵ㣬��
���ɵ㣬��![]() ��
��![]() �����.
�����.
![]()
֪ʶ���ã�
(1)��ͼ 1����![]() ��ʾ������
��ʾ������![]() ����
����![]() ��ʾ������
��ʾ������![]() ����
����![]() ��ʾ������
��ʾ������![]() ����ô��
����ô��![]() �ǣ�
�ǣ�![]() ��( )
��( )
![]()
A.�ɵ� B. ��� C. ��ȷ��
(2)��ͼ 2��![]() Ϊ���������㣬��
Ϊ���������㣬��![]() ����ʾ����Ϊ
����ʾ����Ϊ![]() ����
����![]() ����ʾ����Ϊ
����ʾ����Ϊ![]() ����
����![]() ���ɵ��ʾ������ ��
���ɵ��ʾ������ ��
![]()

��չ����
(3)��ͼ 3��![]() Ϊ���������㣬��
Ϊ���������㣬��![]() ����ʾ����Ϊ
����ʾ����Ϊ![]() ����
����![]() ����ʾ����Ϊ
����ʾ����Ϊ![]() .����һֻ��������P�ӵ�
.����һֻ��������P�ӵ� ![]() ��������ÿ
��������ÿ![]() �뵥λ���ٶ������˶��������
�뵥λ���ٶ������˶��������![]() ֹͣ. ����������ʱ��
ֹͣ. ����������ʱ��![]() ��
�� ![]() ����һ����Ϊ����������ɵ�? (��ֱ��д�����)
����һ����Ϊ����������ɵ�? (��ֱ��д�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽҳ�������һ��ֱ���ܲ�������һ��ʱ��ԭ·���أ��պ��ڵ�16���ӻص����У���С��������t���ӵ��ٶ�Ϊv��/�֣���ҵľ���Ϊs�ף�v��t֮��IJ���ͼ��s��t֮��IJ���ͼ��ֱ���ͼ1��ͼ2��ͼ��û������������ͼ�еĿ���Ȧ��ʾ��������һ�㣩����С�����600��ʱ�����õ�ʱ���ǣ����������ӣ�

A. 4.5B. 8.25C. 4.5 ��8.25D. 4.5 �� 8.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������о��꼶����������״����Ϊ�˳�ȡ��50�����꼶���������������ϸ������ԣ�����������Ƴɱ������£�
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
���� | 1 | 1 | 6 | 18 | 10 | 6 | 2 | 2 | 1 | 1 | 2 |
��1������γ����������ݵ�ƽ��������������λ����
��2����ƽ��������������λ���У�����Ϊ����һ��ͳ������Ϊ���о��꼶��������������Ŀ���Եĺϸ��������Ϊ���ʣ���Ҫ˵�����ɣ�
��3��������н�����3�������꼶���������ݣ�2��������Ϊ�ϸ�ı����Թ��Ƹ��о��꼶��������������Ŀ���Եĺϸ������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������һ�����ѧУ��![]() ��ȫ��ѧ����ѧУͳһ�˳�ȥ�пƼ��ݲι�ѧϰ��Ȼ����ͳһ�˳�ԭ·���أ������ÿͳ�������.���мס���������λ����ͬ�Ŀͳ��������ã����ֿͳ�ÿ�������Ϊ
��ȫ��ѧ����ѧУͳһ�˳�ȥ�пƼ��ݲι�ѧϰ��Ȼ����ͳһ�˳�ԭ·���أ������ÿͳ�������.���мס���������λ����ͬ�Ŀͳ��������ã����ֿͳ�ÿ�������Ϊ![]() Ԫ������ʵ���г�ÿǧ����
Ԫ������ʵ���г�ÿǧ����![]() Ԫ�����ֿͳ�ÿ����ÿǧ��
Ԫ�����ֿͳ�ÿ����ÿǧ��![]() Ԫ�շ�.
Ԫ�շ�.
(1)���г�Ϊ����ǧ��ʱ���������ֿͳ��ķ�����ͬ��
(2)�������һ�����ѧУ���пƼ���Լ![]() �����������꼶�����鳤��Ϊ��ʡ���ã����ѡ�����ֿͳ���
�����������꼶�����鳤��Ϊ��ʡ���ã����ѡ�����ֿͳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����5m������AB��б����һ��ֱ��ǽAO�ϣ���ʱAO�ľ���Ϊ4m��������ӵĶ���A��ǽ�»�1m��C�㣮
��1�������ӵ�B���ƾ���BD�ij��ȣ�
��2������CE��BE�Ĵ�С��ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��a+b��2�����a��b�ǹ���1��ƽ������
��1����3���� ���ǹ���1��ƽ��������4��x���� ���ǹ���1��ƽ�������ú�x�Ĵ���ʽ��ʾ����
��2����a��2x2��3��x2+x����4��b��2x��[3x����4x+x2����2]���ж�a��b�Ƿ��ǹ���1��ƽ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com