
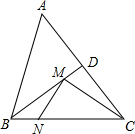
 如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是
如图,在等腰△ABC中,AB=BC=5,AC=6,∠ABC的平分线交AC于点D,M、N分别是BD和BC上的动点,则CM+MN的最小值是| 52-32 |
| AN |
| BD |
| AC |
| BC |
| AN |
| 4 |
| 6 |
| 5 |
| 24 |
| 5 |
| 24 |
| 5 |
| 24 |
| 5 |


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 9 |
| 7 |
| 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
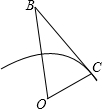 “欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.不过我们现在地球上看到据观测点1000米处的景色,“更上一层楼”中的楼到底有多高呢?存在这样的楼房吗?(设
“欲穷千里目,更上一层楼”是唐代诗人王之涣的不朽诗句.不过我们现在地球上看到据观测点1000米处的景色,“更上一层楼”中的楼到底有多高呢?存在这样的楼房吗?(设 |
| AC |
 |
| AC |
查看答案和解析>>
科目:初中数学 来源: 题型:
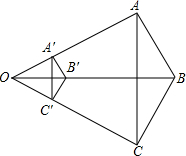 如图,△ABC的三条边与△A′B′C′的三条边满足A′B′∥AB,B′C′∥BC,A′C′∥AC,且OB=3OB′,△ABC的面积与△A′B′C′的面积之间的关系?
如图,△ABC的三条边与△A′B′C′的三条边满足A′B′∥AB,B′C′∥BC,A′C′∥AC,且OB=3OB′,△ABC的面积与△A′B′C′的面积之间的关系?查看答案和解析>>
科目:初中数学 来源: 题型:
| 9 |
| 5 |
| 16 |
| 12 |
| 25 |
| 21 |
| 36 |
| 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com