练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知正六边形ABCDEF和正方形AGHF，则∠ABG的度数为（　　）
    A、75°B、70°
    C、65°D、60°
    考点：多边形内角与外角,等腰三角形的性质
    专题：
    分析：正六边形的每个内角为120°，即可求∠BAF，正方形每个内角为90°，即可求∠GAF，进而求∠BAG的大小，根据AB=AG即可求∠ABG的度数．
    解答：解：∵正六边形的每个内角为120°，正方形每个内角为90°，
    ∴∠BAF=120°，∠GAF=90°，
    ∴∠BAG=30°，
    又∵AB=AG，
    ∴∠ABG=
    180°-30°
    2
    =75°．
    故选：A．
    点评：本题考查了正方形各边长相等，正六边形各内角为120°的性质，考查了等腰三角形底角相等的性质，本题中计算∠BAG=30°是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，高20m的教学楼在一天的某一个时刻在地上的影子长15m，在教学楼前10m处有一高为5m的国旗杆，试问在这一时刻你能看到国旗的影子吗？通过计算说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一元二次方程2x（kx-4）-x2+6=0有实根，k的最大整数是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，△OBC的顶点O（0，0），B（-6，0），且∠OCB=90°，OC=BC，则点C关于y轴对称的点的坐标是（　　）
    A、（3，3）
    B、（-3，3）
    C、（-3，-3）
    D、（
    		18
    ，
    		18
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    数学老师布置10道选择题作为课堂练习，学习委员将全班同学的答题情况绘制成如下条形统计图，根据统计图可知，答对8道题的同学的频率是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，线段AB=8cm，C是线段AB上一点，AC=3.2cm，M是AB的中点，N是AC的中点．
    （1）图中共有
     
    条线段．
    （2）求线段MN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

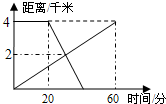    已知A、B两地相距4千米，上午8：00，甲从A地出发到B地，8：20乙从B地出发骑自行车到A地，甲，乙两人离A地的距离（千米）与甲所用的时间（分）之间的关系如图所示，由图中的信息可知，乙的速度为（单位：千米/小时）（　　）
    A、4B、6C、8D、12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线l1：y1=-x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l1上一点，另一直线l2：y2=
    1
    2
    x+b过点P．
    （1）求点P坐标和b的值；
    （2）若点C是直线l2与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．
    ①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；
    ②求出t为多少时，△APQ的面积小于3；
    ③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    2013年国庆节下雨的概率是0.99，则“2013年国庆节下雨”是
     
    事件．

    查看答案和解析>>

    同步练习册答案