
【题目】已知菱形![]() 的对角线交于点
的对角线交于点![]() 是直线
是直线![]() 上任意一点(异于点
上任意一点(异于点![]() ),过点
),过点![]() 作平行于
作平行于![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当点![]() 在线段
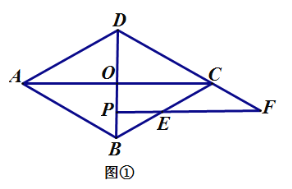
在线段![]() 上时,如图 ①,易证:
上时,如图 ①,易证:![]() (不用证明);
(不用证明);
(2)当点![]() 在线段
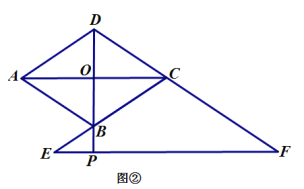
在线段![]() 的延长线上时,如图 ②;当点
的延长线上时,如图 ②;当点![]() 在线段
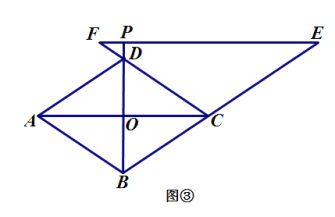
在线段![]() 的延长线上时,如图 ③,线段
的延长线上时,如图 ③,线段![]() 之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
【答案】(1)证明详见解析;(2)图②的结论为![]() ;图③的结论为
;图③的结论为![]() ;详见解析.
;详见解析.
【解析】
(1)先解直角三角形AOB得出AO=![]() ,由菱形的性质得到AC=
,由菱形的性质得到AC=![]() ,延长FP交AB于点G,证明四边形AGFD是平行四边形得到AC=FG,再证明PE=PG即可得到答案;
,延长FP交AB于点G,证明四边形AGFD是平行四边形得到AC=FG,再证明PE=PG即可得到答案;
(2)在②中延长FE交BC的延长线于G,可证得PF=PG,再证明四边形ACGE为平行四边形可得AC=EG,可证得![]() ;在③中,延长CB交EF于点G,可证明PG=PF,可得到
;在③中,延长CB交EF于点G,可证明PG=PF,可得到![]()
(1)∵四边形ABCD是菱形,∠DAB=60°,
∴∠OAB=30°,∠AOB=90°,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
延长FP交AB于点G,

∵AB//CD,AC//FG
∴四边形ACFG是平行四边形,
∴AC=FG(平行四边形的对边相等)
∵EG//AC,
∴![]() (被平行线所截的线段对应成比例)
(被平行线所截的线段对应成比例)
又∵OA=OC
∴PE=PG,
∴AC=FG=PF+PG=PE+PF
∴![]()
![]() )当P在DB的延长线上时,如图②,结论为
)当P在DB的延长线上时,如图②,结论为![]()
证明:延长FE交DA的延长线于点G,

∵AC∥FG,
∴![]() ,
,
∵四边形ABCD为菱形,
∴AO=CO,
∴PF=PG,
∴EG=PG-PE=PF-PE,
又∵AB∥CG,AC∥EG,
∴四边形ACEG为平行四边形,
∴AC=EG,
∴AC=PF-PE,
![]()
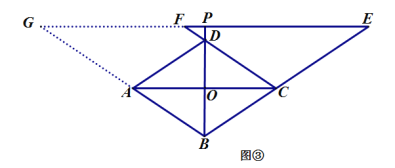
当P在BD的延长线上时,如图③,结论为![]()
延长EF交BA的延长线于点G,
∵AC∥EF,
∴![]() ,
,
∵四边形ABCD为菱形,
∴AO=CO,
∴PG=PE,
∴FG=PG-PF=PE-PF,
又∵AC∥EG,AG∥CF,
∴四边形AGFC为平行四边形,
∴FG=AC,
∴AC=PE-PF,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在城市改造中,市政府欲在一条人工河上架一座桥,河的两岸PQ与MN平行,河岸MN上有A、B两个相距50米的凉亭,小亮在河对岸D处测得∠ADP=60°,然后沿河岸走了110米到达C处,测得∠BCP=30°,求这条河的宽.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
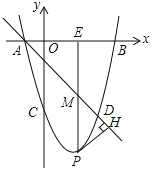
(1)求抛物线的解析式:
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李去买套装![]() 色水笔和笔记本,若购买
色水笔和笔记本,若购买![]() 袋笔和
袋笔和![]() 本笔记本,他身上的钱还差
本笔记本,他身上的钱还差![]() 元,若改 成购买
元,若改 成购买![]() 袋笔和
袋笔和![]() 本笔记本,他身上的钱会剩下
本笔记本,他身上的钱会剩下![]() 元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
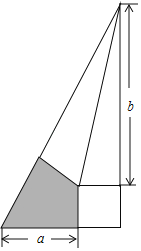
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,以点
,以点![]() 为顶点作
为顶点作![]() ,使得
,使得![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
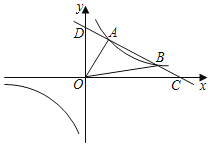
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装加工厂甲、乙两个车间共同加工一款休闲装,且每人每天加工的件数相同,甲车间比乙车间少10人,甲车间每天加工服装400件,乙车间每天加工服装600件.
(1)求甲、乙两车间各有多少人;
(2)甲车间更新了设备,平均每人每天加工的件数比原来多了10件,乙车间的加工效率不变,在两个车间总人数不变的情况下,加工厂计划从乙车间调出一部分人到甲车间,使每天两个车间加工的总数不少于1314件,求至少要从乙车间调出多少人到甲车间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com