练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若二次函数y=ax2-2ax+c的图象经过点A(0，-1)，B(-2，y1)，C(3，y2)，D(，y3)，且与x轴没有交点，则y1，y2，y3，的大小关系是（ ）

    A.y1>y2>y3B.y1> y3> y2C.y2> y1>y3D.y3>y2> y1

    【答案】D

    【解析】

    先利用抛物线过A点，与x轴没有交点可判断a＜0，再求出抛物线的对称轴为直线x=1，接着比较B、C、D三点到直线x=1的距离大小，然后根据二次函数的性质可判断y1，y2，y3的大小关系．

    ∵抛物线过A（0，-1），而抛物线与x轴没有交点，
    ∴抛物线开口向下，即a＜0，
    ∵抛物线的对称轴为直线x==1，
    而B点到直线x=1的距离最大，D点到直线x=1的距离最小，
    ∴y1＜y2＜y3．
    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC交AC于点E，AC的反向延长线交⊙O于点F．

    (1)试判断直线DE与⊙O的位置关系，并说明理由；

    (2)若∠C＝30°，⊙O的半径为6，求弓形AF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题解决）

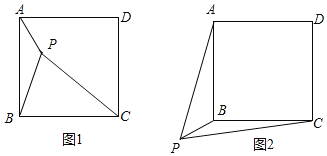
    一节数学课上，老师提出了这样一个问题：如图1，点P是正方形ABCD内一点，PA=1，PB=2，PC=3．你能求出∠APB的度数吗？

    小明通过观察、分析、思考，形成了如下思路：

    思路一：将△BPC绕点B逆时针旋转90°，得到△BP′A，连接PP′，求出∠APB的度数；

    思路二：将△APB绕点B顺时针旋转90°，得到△CP'B，连接PP′，求出∠APB的度数．

    请参考小明的思路，任选一种写出完整的解答过程．

    （类比探究）

    如图2，若点P是正方形ABCD外一点，PA=3，PB=1，PC=，求∠APB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A,C,E在同一直线上.

    （1）求坡底C点到大楼距离AC的值；

    （2）求斜坡CD的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年九龙口诗词大会在九龙口镇召开，我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作．本次学生志愿者工作一共设置了三个岗位，分别是引导员、联络员和咨询员．

    （1）若要从这5名志愿者中随机选取一位作为引导员，求选到女生的概率；

    （2）若甲、乙两位志愿者都从三个岗位中随机选择一个，请你用画树状图或列表法求出他们恰好选择同一个岗位的概率．（画树状图和列表时可用字母代替岗位名称）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小西红柿又叫圣女果，既可以生吃，也可以作为美食原料，营养价值极高，因此深受人们的欢迎，为了解甲、乙两个规模相当的种植基地的小西红柿产量，从这两个种植基地中各随机选取50株小西红柿秧苗进行调查，将得到的数据分类整理成如下统计表：

    甲基地每株秧苗收获小西红柿个数统计表：

    小西红柿个数x／个

    25≤x＜35

    35≤x＜45

    45≤x＜55

    55≤x＜65

    65≤x＜75

    75≤x＜85

    秧苗株数／株

    4

    8

    12

    12

    10

    4

    乙基地每株秧苗收获小西红柿个数统计表：

    小西红柿个数

    x／个

    25≤x＜35

    35≤x＜45

    45≤x＜55

    55≤x＜65

    65≤x＜75

    75≤x＜85

    秧苗株数／株

    9

    6

    12

    10

    11

    2

    （说明：x＜45为产量不合格，x≥45为产量合格，其中45≤x＜65为产量良好，65≤x＜85为产量优秀）

    （）以这50株小西红柿秧苗收获小西红柿个数为样本，现从乙基地调查的50株秧苗中随机抽取一株，估计“秧苗产量合格”的概率；

    （2）某水果商准备在甲、乙两个小西红柿种植基地中选择一个进行合作，若一株秧苗产量优秀可获利13元，产量良好可获利8元，产量不合格亏损5元．以这两个基地的50株秧苗获得的平均利润为决策依据，请你利用所学的统计知识帮该水果商选择与哪个基地进行合作能获得更大利润？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】河西中学九年级共有9个班，300名学生，学校要对该年级学生数学学科学业水平测试成绩进行抽样分析，请按要求回答下列问题：

    （1）（收集数据）若从所有成绩中抽取一个容量为36的样本，以下抽样方法中最合理的是________．

    ①在九年级学生中随机抽取36名学生的成绩；

    ②按男、女各随机抽取18名学生的成绩；

    ③按班级在每个班各随机抽取4名学生的成绩．

    （2）（整理数据）将抽取的36名学生的成绩进行分组，绘制频数分布表和成绩分布扇形统计图如下．请根据图表中数据填空：

    成绩（单位：分）

    频数

    频率

    A类（80～100）

    18

    B类（60～79）

    9

    C类（40～59）

    6

    D类（0～39）

    3

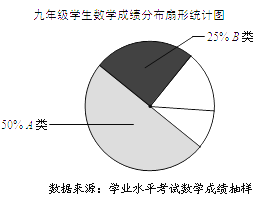
    ①C类和D类部分的圆心角度数分别为________°、________°；

    ②估计九年级A、B类学生一共有________名．

    （3）（分析数据）教育主管部门为了解学校教学情况，将河西、复兴两所中学的抽样数据进行对比，得下表：

    学校

    平均数（分）

    极差（分）

    方差

    A、B类的频率和

    河西中学

    71

    52

    432

    0.75

    复兴中学

    71

    80

    497

    0.82

    你认为哪所学校本次测试成绩较好，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

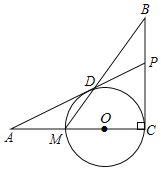
    【题目】如图，已知BC⊥AC，圆心O在AC上，点M与点C分别是AC与⊙O的交点，点D是MB与⊙O的交点，点P是AD延长线与BC的交点，且ADAO＝AMAP．

    （1）连接OP，证明：△ADM∽△APO；

    （2）证明：PD是⊙O的切线；

    （3）若AD＝12，AM＝MC，求PB和DM的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＝4，BC＝6，点E是AB中点，在AD上取一点G，以点G为圆心，GD的长为半径作圆，该圆与BC边相切于点F，连接DE，EF，则图中阴影部分面积为（　　）

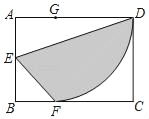
    A. 3πB. 4πC. 2π+6D. 5π+2

    查看答案和解析>>

    同步练习册答案