

|
|
 (2)DE=PE.
(2)DE=PE.
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.
如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.
在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.查看答案和解析>>
科目:初中数学 来源: 题型:
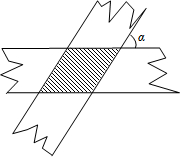 如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )
如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com