
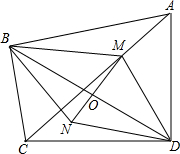
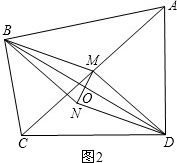
 已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.
已知:如图所示,四边形ABCD中∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO并延长MO到N,使NO=MO,连接BN与ND.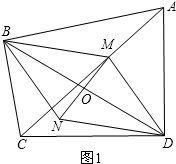


科目:初中数学 来源: 题型:
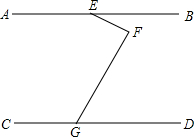 (1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.
(1)如图AB∥CD,试判断∠BEF、∠EFG、∠FGD之间的关系.并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
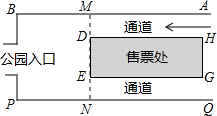 如图,公园入口处前有一间售票处,其屋面DEGH是矩形.售票处后墙DE与两侧通道垂直.小亮的爸爸已购公园门票,在点P处等候小亮,小亮沿售票处北侧的通道中央行进,去找爸爸.
如图,公园入口处前有一间售票处,其屋面DEGH是矩形.售票处后墙DE与两侧通道垂直.小亮的爸爸已购公园门票,在点P处等候小亮,小亮沿售票处北侧的通道中央行进,去找爸爸.查看答案和解析>>
科目:初中数学 来源: 题型:
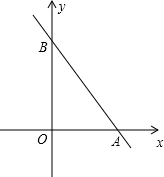 直线y=-
直线y=-| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com