
如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
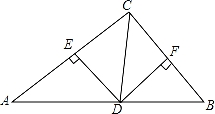
4 .
【考点】角平分线的性质.
【专题】压轴题.
【分析】首先根据CD平分∠ACB交AB于点D,可得∠DCE=∠DCF;再根据DE⊥AC,DF⊥BC,可得∠DEC=∠DFC=90°,然后根据全等三角形的判定方法,判断出△CED≌△CFD,即可判断出DF=DE;最后根据三角形的面积=底×高÷2,求出△BCD的面积是多少即可.
【解答】解:∵CD平分∠ACB交AB于点D,
∴∠DCE=∠DCF,
∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,
在△DEC和△DFC中,
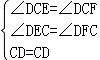 (AAS)
(AAS)
∴△DEC≌△DFC,
∴DF=DE=2,
∴S△BCD=BC×DF÷2
=4×2÷2
=4
答:△BCD的面积是4.
故答案为:4.
【点评】(1)此题主要考查了角平分线的性质和应用,要熟练掌握,解答此题的关键是要明确:角的平分线上的点到角的两边的距离相等.
(2)此题还考查了全等三角形的判定和性质的应用,以及三角形的面积的求法,要熟练掌握.


科目:初中数学 来源: 题型:
四张扑克牌的牌面如图1所示,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.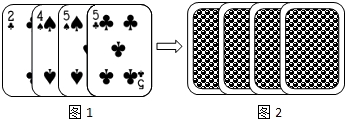
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列等式:
①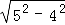 =1×3;②
=1×3;②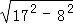 =3×5;③
=3×5;③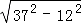 =5×7;
=5×7;
…
根据上述规律解决下列问题:
(1)完成第④个等式: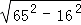 = × ;
= × ;
(2)写出你猜想的第n个等式(用含n的式子表示),并证明其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形ABCD中,AB=3cm,AD=4cm,以A为圆心,4cm为半径作⊙A,则( )
A.B在⊙A内,C在⊙A外 B.D在⊙A内,C在⊙A外
C.B在⊙A内,D在⊙A外 D.B在⊙A上,C在⊙A外
查看答案和解析>>
科目:初中数学 来源: 题型:
一个口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4,随机地摸出一个小球,然后放回,再随机地摸出一个小球,则两次摸出的小球标号的和等于4的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com