考点:平行线的性质
专题:
分析:(1)连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(2x°+2y°),求出∠AEC=2(x°+y°),∠AFC═x°+y°,即可得出答案.
(2)连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(3x°+3y°),求出∠AEC=3(x°+y°),∠AFC═2(x°+y°),即可得出答案.
(3)由(1)(2)可知∠AFC与∠AEC的数量关系是:∠AFC=
∠AEC.
解答: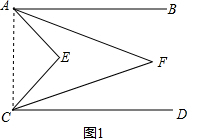
解:(1)如图1,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+2x°+∠ACE+2y°=180°,
∴∠CAE+∠ACE=180°-(2x°+2y°),∠FAC+∠FCA=180°-(x°+y°)
∴∠AEC=180°-(∠CAE+∠ACE)
=180°-[180°-(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(x°+y°)]
=x°+y°
∴∠AFC=
∠AEC,
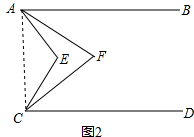
(2)如图2,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x°+∠ACE+3y°=180°,
∴∠CAE+∠ACE=180°-(3x°+3y°),∠FAC+∠FCA=180°-(2x°+2y°)
∴∠AEC=180°-(∠CAE+∠ACE)
=180°-[180°-(3x°+3y°)]
=3x°+3y°
=3(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)
=180°-[180°-(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∴∠AFC=
∠AEC,
(3)若∠AFC=
∠EAB,∠ECF=
∠ECD,则∠AFC与∠AEC的数量关系是:∠AFC=
∠AEC;
点评:本题考查了平行线性质和三角形内角和定理的应用,注意:两直线平行,同旁内角互补.


 解:(1)如图1,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
解:(1)如图1,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,


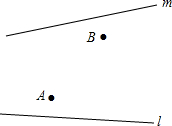 如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m为直线).
如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m为直线).