
【题目】如图,在△ABC中,∠C=900,AC=BC,AE平分∠BAC与BC交于点E, DE⊥AB于点D,若AB=8cm,则△DEB的周长为( )

A.4cmB.6cmC.8cmD.10cm
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
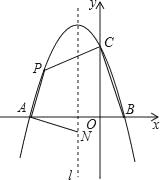
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
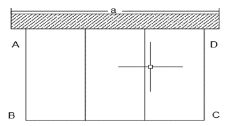
【题目】如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长![]() 米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
(1)若墙长![]() 米,求AB、BC的长.
米,求AB、BC的长.
(2)若![]() 米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象的对称轴是直线
的图象的对称轴是直线![]() ,其图象的一部分如图所示则:①
,其图象的一部分如图所示则:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤当
;⑤当![]() 时,
时,![]() .其中判断正确的有( )个.
.其中判断正确的有( )个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.

解法探究:小明同学通过思考,得到了如下的解决方法.
延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,从而可得结论.
(1)请先写出小明得出的结论,并在小明的解决方法的提示下,写出所得结论的理由.
解:线段BE、EF、FD之间的数量关系是: .
理由:延长FD到点G,使DG=BE,连结AG.(以下过程请同学们完整解答)
(2)拓展延伸:
如图②,在四边形ABCD中,AB=AD,若∠B+∠D=180°,E、F分别是BC、CD上的点.且∠EAF=![]() ∠BAD,则(1)中的结论是否仍然成立?若成立,请再把结论写一写;若不成立,请直接写出你认为成立的结论.
∠BAD,则(1)中的结论是否仍然成立?若成立,请再把结论写一写;若不成立,请直接写出你认为成立的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com