
请完成下面的说明:(1)如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°- ∠A.
∠A.
说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____.
根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,
所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.
根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.
∠_______.
所以∠BGC=180°-(∠2+∠3)=90°-∠____.
(2)如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+ ∠A.
∠A.
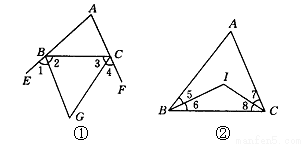
(3)用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?
(1)A A A A A A;(2)证明见解析;(3)∠BGC和∠BIC互补.
【解析】
试题分析:(1)先根据三角形内角和定理可得出∠ABC+∠ACB=180°-∠A,再由平角的定义可得出∴∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A,根据角平分线的定义即可得出结论;
(2)先根据三角形内角和等于180°可知∠ABC+∠ACB=180°-∠A,再由△ABC的内角平分线交于点I,
可知∠6+∠7= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)=90°-
(180°-∠A)=90°- ∠A,故有∠BIG=180°-(∠6+∠8)即可得出结论.
∠A,故有∠BIG=180°-(∠6+∠8)即可得出结论.
(3)直接把两角相加即可得出结论.
试题解析:(1)∵根据三角形内角和等于180°,
∴∠ABC+∠ACB=180°-∠A.
∵平角是180°,
∴∠ABE+∠ACF=180°×2=360°,
∴∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A.
∵△ABC的外角平分线交于G,
∴∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠A)=90°+
(180°+∠A)=90°+ ∠A,
∠A,
∴∠BGC=90°- ∠A.
∠A.
(2)证明:∵三角形内角和等于180°,
∴∠ABC+∠ACB=180°-∠A,
∵△ABC的内角平分线交于点I,
∴∠6+∠7= (∠ABC+∠ACB)=
(∠ABC+∠ACB)= (180°-∠A)=90°-
(180°-∠A)=90°- ∠A,
∠A,
∴∠BIC=180°-(∠6+∠8)
=180°-(90°- ∠A)
∠A)
=90°+ ∠A,
∠A,
即∠BIC=90°+ ∠A;
∠A;
(3)【解析】
∵由(1)、(2)知∠BGC=90°- ∠A,BIC=90°+
∠A,BIC=90°+ ∠A,
∠A,
∴∠BGC+∠BIC=90°- ∠A+90°+
∠A+90°+ ∠A=180°,
∠A=180°,
∴∠BGC和∠BIC互补.
考点:1.三角形内角和定理;2.三角形的角平分线、中线和高.


科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次模拟数学试卷(解析版) 题型:解答题
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,∠AOB′的度数是( )

A.25° B.30° C.35° D.40°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省宣城市泾县琴溪片九年级上学期期中联考数学试卷(解析版) 题型:选择题
如图所示,抛物线y=ax2-x+c 的对称轴是直线x=1
的对称轴是直线x=1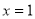 ,且图像经过点
,且图像经过点 (3,0),则
(3,0),则 的值为( )
的值为( )
A、0 B、 -1 C、 1 D、 2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津宝坻王卜庄镇初中八年级上学期期中考试数学试卷(解析版) 题型:填空题
已知△ABC的三边长a、b、c,化简│a+b-c│-│b-a-c│的结果是_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏东台苏东双语八年级上学期第一次质检数学试卷(解析版) 题型:解答题
如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①② ③;(2)①③
③;(2)①③ ②;(3)②③
②;(3)②③ ①.
①.

(1)以上三个命题是真命题的为(直接写号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏启东南苑中学七年级上学期第一单元测试数学试卷(解析版) 题型:选择题
从数6,-1,15,-3中,任取三个不同的数相加,所得到的结果中最小的是( )
A.-3 B.-1 C.3 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com