
 已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).
已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).分析 (1)根据给出的抛物线的解析式并且结合函数的图象写出三条不同的结论即可;
(2)先将a=$\frac{1}{2}$代入抛物线解析式,分别求得M、N、E、F四点坐标,再根据四点坐标写出合理的结论;
(3)根据题意求出CD关于x的解析式,然后求出当x=0时,CD的值最大.
解答 解:
(1)答案不唯一,只要合理均可.例如:
①抛物线y1=-ax2-ax+1开口向下,或抛物线y2=ax2-ax-1开口向上;
②抛物线y1=-ax2-ax+1的对称轴是x=-$\frac{1}{2}$,或抛物线y2=ax2-ax-1的对称轴是x=$\frac{1}{2}$;
③抛物线y1=-ax2-ax+1经过点(0,1),或抛物线y2=ax2-ax-1经过点(0,-1);
④抛物线y1=-ax2-ax+1与y2=ax2-ax-1的形状相同,但开口方向相反;
⑤抛物线y1=-ax2-ax+1与y2=ax2-ax-1都与x轴有两个交点;
⑥抛物线y1=-ax2-ax+1经过点(-1,1)或抛物线y2=ax2-ax-1经过点(1,-1);
(2)当a=$\frac{1}{2}$时,y1=-$\frac{1}{2}$x2-$\frac{1}{2}$x+1,令0=-$\frac{1}{2}$x2-$\frac{1}{2}$x+1,
解得xM=-2,xN=1.
y2=$\frac{1}{2}$x2-$\frac{1}{2}$x-1,令0=$\frac{1}{2}$x2-$\frac{1}{2}$x-1,解得xE=-1,xF=2.
①∵xM+xF=0,xN+xE=0,
∴点M与点F关于x轴对称,点N与点E关于x轴对称;
②∵xM+xF+xN+xE=0,
∴M,N,E,F四点横坐标的代数和为0;
③∵MN=3,EF=3,
∴MN=EF(或ME=NF);
(3)∵a>0,
∴抛物线y1=-ax2-ax+1开口向下,抛物线y2=ax2-ax-1开口向上.
根据题意,得CD=y1-y2=(-ax2-ax+1)-(ax2-ax-1)=-2ax2+2.
∴当x=0时,CD的最大值是2.
点评 本题是二次函数的综合题,题中涉及抛物线的性质以及最值的求法等知识点,解题时要注意数形结合数学思想的运用,是各地中考的热点和难点,同学们要加强训练,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )| A. | 0.5米 | B. | 0.6米 | C. | 0.3米 | D. | 0.9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
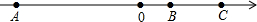 如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,
如图:已知A、B、C是数轴上的三点,点C表示的数是6,BC=4,AB=12,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
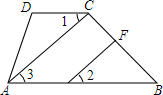 如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程.
如图,在四边形ABCD中,∠BCD+∠B=180°,AC⊥CB于C,EF⊥CB于F,∠1和∠2相等吗?请完成下面的说理过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 242 | B. | 248 | C. | 254 | D. | 258 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
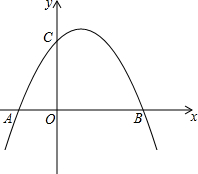 如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.
如图所示,抛物线y=ax2+x+c(a≠0)与x轴交于点A(-2,0)、点B(6,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,该图形由6个完全相同的小正方形排列而成.
如图,该图形由6个完全相同的小正方形排列而成.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一只蚂蚁沿着一个长方体表面从点A出发,经过3个面爬到点B,已知底面是边长为2的正方形,高为8,如果它运动的路径是最短的,则最短路径的长为10.
如图,一只蚂蚁沿着一个长方体表面从点A出发,经过3个面爬到点B,已知底面是边长为2的正方形,高为8,如果它运动的路径是最短的,则最短路径的长为10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com