
【题目】如图,⊙O的半径为![]() ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
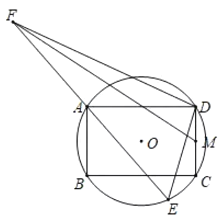
【答案】![]()
【解析】
如图,连接AC交BD于点O,以AD为边向上作等边△ADJ,连接JF,JA,JD,JM.判断出点F的运动轨迹,即可解决问题.
解:如图,连接AC交BD于点O,以AD为边向上作等边△ADJ,连接JF,JA,JD,JM.
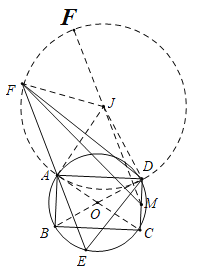
∵四边形ABCD是矩形,
∴∠ADC=90°,
∵AD=6,AC=![]() ,
,
∴sin∠ACD=![]() ,
,
∴∠ACD=60°,
∴∠FED=∠ACD=60°,
∵DF⊥DE,
∴∠EDF=90°,
∴∠EFD=30°,
∵△JAD是等边三角形,
∴∠AJD=60°,
∴∠AFD=![]() ∠AJD,
∠AJD,
∴点F的运动轨迹是以J为圆心JA为半径的圆,
∴当点F在MJ的延长线上时,FM的值最大,
此时FJ=6,JM=![]() ,
,
则FM的最大值为![]() ;
;
故答案为:![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,以点
,以点![]() 为顶点作
为顶点作![]() ,使得
,使得![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会已于2010年4月30日开幕,各国游客都被吸引到了这个地方,据统计到5月10号为止最高单日接待量已达到100万人次,其中中国馆自然是最受欢迎的展馆,在世博会开园第一天共接待了游客3万余人,而外国场馆中最受欢迎的依次是瑞士馆、法国馆、德国馆、西班牙馆、日本馆.现将某天世博会最受欢迎的6个馆的参观人数用统计图①②分别表示如下:
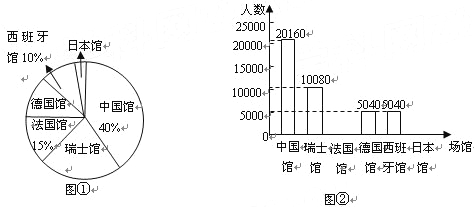
请根据统计图回答下列问题:
(1)这一天参观这6个场馆的总人数为 __ ,其中参观日本馆的人数有__,德国馆所在扇形的圆心角度数为__;
(2)请将条形统计图补充完整;
(3)小宝和小贝都想利用暑假去上海参观世博会,恰好张伯伯有一张世博会的门票,小宝和小贝都想得到这张门票.于是他们决定用转转盘的游戏来决定这张票由谁获得,游戏规则如下:将一质地均匀的转盘等分成5个面积相等的扇形,上面分别标有数字 -l,4,5,-6,0,小宝和小贝均随机地转转盘一次,把指针指向区域内的数字分别记为x、y.若指针指在边界,则重新转一次直到指针指向一个区域内为止,然后他们计算出xy的值.规定:当xy的值为负数时,门票归小宝;xy的值为正数时,门票归小贝.请利用表格或树状图游戏对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装加工厂甲、乙两个车间共同加工一款休闲装,且每人每天加工的件数相同,甲车间比乙车间少10人,甲车间每天加工服装400件,乙车间每天加工服装600件.
(1)求甲、乙两车间各有多少人;
(2)甲车间更新了设备,平均每人每天加工的件数比原来多了10件,乙车间的加工效率不变,在两个车间总人数不变的情况下,加工厂计划从乙车间调出一部分人到甲车间,使每天两个车间加工的总数不少于1314件,求至少要从乙车间调出多少人到甲车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置P的铅直高度PB.(测倾器高度忽略不计,结果保留根号形式)

查看答案和解析>>
科目:初中数学 来源: 题型:
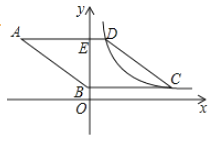
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(1)求出k值.
(2)求出△OCD的面积
(3)试探究坐标轴上是否存在点P,使得△PCD的面积等于菱形ABCD的面积的一半,如果存在,请直接写出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF,有以下结论:
①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,![]() ;④BE+DF=EF;⑤若点F是DC的中点,则CE
;④BE+DF=EF;⑤若点F是DC的中点,则CE![]() CB.
CB.
其中正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
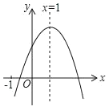
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
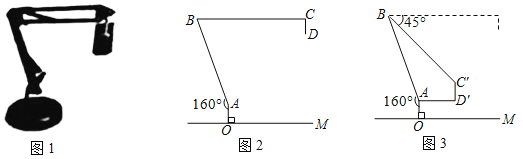
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com