
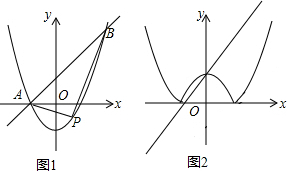
���� ��1����k=1���������߽���ʽ��ֱ�߽���ʽ�����������飬�����������A��B�����ꣻ
��2������P��y��ƽ���ߣ���������ABP�ָ������С�����Σ���PFΪ�ף������������θߵĺ�ΪAB�����ˮƽ���룬������������������
��3����ͼ���۵������ֱ���뷭�ۺ�����������е���������������飬���kֵ�����k��0���������k��ȡֵ��Χ��
��� �⣺��1����k=1ʱ�������ߵĽ���ʽΪy=x2-1��ֱ�ߵĽ���ʽΪy=x+1��
����ֱ���������ߣ��ã�
$\left\{\begin{array}{l}{y=x+1}\\{y={x}^{2}-1}\end{array}\right.$��
���x1=-1��x2=2��
��x=-1ʱ��y-x+1=0����x=2ʱ��y=x+1=3��
��A��-1��0����B��2��3����
��2����P��x��x2-1������ͼ��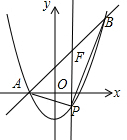
����P��PF��y�ᣬ��ֱ��AB��F��
��F��x��x+1����
PF=yF-yP=��x+1��-��x2-1��=-x2+x+2��
S��ABP=S��PFA+S��PFB=$\frac{1}{2}$PF��xF-xA��+$\frac{1}{2}$PF��xB-xF��$\frac{3}{2}$PF��
S��ABP=$\frac{3}{2}$��-x2+x+2��=-$\frac{3}{2}$��x-$\frac{1}{2}$��2+$\frac{27}{8}$
�ߵ�x=$\frac{1}{2}$ʱ��yP=��$\frac{1}{2}$��2-1=-$\frac{3}{4}$��
���ABP��������ֵΪ$\frac{27}{8}$��
��ʱ��P�����꣨$\frac{1}{2}$��-$\frac{3}{4}$����
��3������ͼ��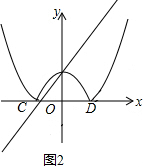
������y=0��
x2+��k-1��x-k=0��
������x+k����x-1��=0��
x=-k����x=1��
C��-k��0����D��1��0����
ֱ��y=kx+1����0��1����
��������y=x2+��k-1��x-k����x��Գƣ�
�ã�y=-x2-��k-1��x+k
����ֱ��y=kx+1���ã�
x2+��2k-1��x+1-k=0
��=��2k-1��2-4��1-k��=0
�ã�k=$\frac{\sqrt{3}}{2}$���ᣩ��k=-$\frac{\sqrt{3}}{2}$��
��k��0��
��0��k��$\frac{\sqrt{3}}{2}$��
��ֱ��y=kx+1������C��-1��0��ʱ��k=1��
����ͼ���֪��0��k��$\frac{\sqrt{3}}{2}$��k��1ʱ��ֱ��y=kx+1�����ͼ��ֻ�����������㣮
���� ��Ŀ�����˶��κ����ۺ�Ӧ�ã�ͨ����ֱ�ߡ������߽���ʽ����⣬����������������⼰ֱ���������ߵ�λ�ù�ϵ���������ѧ�����ۺ�ѹ�����ˮƽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ȵ������Ե�Բ�Ľ���� | B�� | ��ȵ������ԵĻ���� | ||
| C�� | ��ȵĻ����Ե������ | D�� | ��ȵ�Բ�Ľ����ԵĻ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ABC�У�DΪBC����һ�㣬��AB=13cm��BD=5cm��AD=12cm��BC=14cm����AC�ij���
��ͼ��ʾ����ABC�У�DΪBC����һ�㣬��AB=13cm��BD=5cm��AD=12cm��BC=14cm����AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com