练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    等腰三角形的两边长分别为3cm和7cm，则周长为（　　）cm．
    A、13B、17
    C、13或17D、17或11
    考点：等腰三角形的性质,三角形三边关系
    专题：
    分析：题中没有指明哪个是底哪个腰，故应该分两种情况进行分析，注意利用三角形三边关系进行检验．
    解答：解：当7为腰时，周长=7+7+3=17；
    当3为腰时，因为3+3＜7，所以不能构成三角形；
    故三角形的周长是17．
    故选B．
    点评：本题考查的是等腰三角形的性质，在解答此题时要进行分类讨论．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

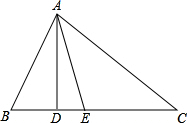    如图，在△ABC中，∠B＞∠C，AD⊥BC，AE平分∠BAC．
    （1）若∠B=70°，∠C=30°．
    ①求∠BAE=
     
    °；
    ②∠DAE=
     
    °．
    （2）探究：小明认为如果只要知道∠B-∠C=n°，就能求出∠DAE的度数？请你就这个问题展开探究：
    ①实验：填表
    ∠B的度数∠C的度数∠DAE的度数
    70°30°（此格不需填写）
    65°25°
     
    50°20°
     
    80°56°
     
    ②结论：当∠B-∠C=n°时，试用含n的代数式表示∠DAE的度数，并写出推导过程；
    ③应用：若∠A=56°，∠DAE=12°，则∠B=
     
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

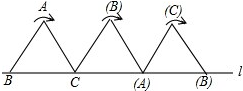    将边长为1cm的等边三角形ABC沿直线l向右翻动（不滑动），点B从开始到结束，所经过路径的长度为（　　）
    A、
    4
    3
    πcm
    B、（2+
    2
    3
    ）πcm
    C、πcm
    D、2
    		2
    cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

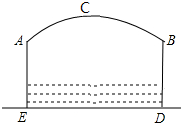    如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED=16m，AE=8m，抛物线的顶点C到ED的距离是11m．试以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系，求题中抛物线的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知∠AOB=30°，点P在∠AOB的内部，点C与点P关于OB对称，点D与点P关于OA对称，则△OCD是（　　）
    A、等腰三角形
    B、等边三角形
    C、直角三角形
    D、钝角三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    为了解城市居民日常出行使用交通工具方式的情况，进行了问卷调查，共收回600份调查问卷，结果统计如下：
    出行方式坐公交车骑自行车、电动车开私家车坐单位班车
    人数2502707010
    根据以上调查结果，制作扇形统计图表示使用交通工具的人数占总调查人数的百分比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    （1）（
    1
    2
    ）-2-（
    		3
    -
    		2
    ）0+2sin60°-|-3|
    （2）（
    a2
    a-2
    -
    1
    a-2
    ）÷
    a2-2a+1
    a-2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：二次函数y=x2-4x+3．
    （1）求出该二次函数图象的对称轴和顶点坐标；
    （2）求出该抛物线与x轴的交点坐标；
    （3）当x取何值时，y＜0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：
    		9
    -(-
    1
    5
    )0    +（-1）2012
    （2）解方程：（x-1）2=9．

    查看答案和解析>>

    同步练习册答案