
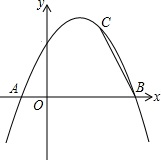
 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
(4-1)2+(
|
| ||
| 2 |
(-1)2+(y-
|
| ||
| 2 |
9+
| ||
| 2 |
9-
| ||
| 2 |
9+
| ||
| 2 |
9-
| ||
| 2 |
| (0-4)2+y2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(-1)2+(y-
|
| (0-4)2+y2 |
| 7 |
| 12 |
| 7 |
| 12 |
9+
| ||
| 2 |
9-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 7 |
| 12 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
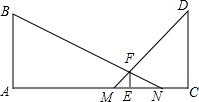 如图所示,晚上小亮走在大街上,他发现当他站在大街上高度相等的两盏路灯AB和CD之间时,自己右边的影子NE的长为3m,左边的影子ME的长为1.5m,又知小亮的身高EF为1.80m,两盏路灯AC之间的距离为12m,点A、M、E、N、C在同一条直线上,问:路灯的高为多少米?
如图所示,晚上小亮走在大街上,他发现当他站在大街上高度相等的两盏路灯AB和CD之间时,自己右边的影子NE的长为3m,左边的影子ME的长为1.5m,又知小亮的身高EF为1.80m,两盏路灯AC之间的距离为12m,点A、M、E、N、C在同一条直线上,问:路灯的高为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
| 6,8,10 | 62+82=102 |
| 8,15,17 | 82+152=172 |
| 10,24,26 | 102+242=262 |
| … | … |
| 20,b,c | 202+b2=c2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com