
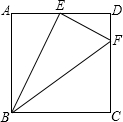
 在正方形ABCD中,点E为AD中点,DF=$\frac{1}{4}$CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正确的有( )
在正方形ABCD中,点E为AD中点,DF=$\frac{1}{4}$CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为$\frac{1}{2}$AB;(4)$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据正方形的性质得到AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,由于点E为AD中点,DF=$\frac{1}{4}$CD,于是得到$\frac{AB}{DE}=\frac{AE}{DF}$=2,推出△ABE∽△DEF,根据相似三角形的性质得到∠ABE=∠DEF,根据平角的定义得到∠BEF=90°,于是求得BE⊥EF;故①正确;根据相似三角形的性质得到$\frac{AB}{DE}=\frac{BE}{EF}$,等量代换得到$\frac{AB}{AE}=\frac{BE}{EF}$,推出△ABE∽△BEF,于是得到△ABE∽△BEF∽△DEF,即可得到图中有3对相似三角形;故②正确;根据相似三角形的性质得到∠ABE=∠EBF,根据角平分线的性质得到E到BF的距离=AE,于是得到E到BF的距离为$\frac{1}{2}$AB;故③正确;设DF=1,则AE=DE=2,AB=BC=CD=4,由勾股定理得到BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=2$\sqrt{5}$,EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{5}$,求得S△BEF=$\frac{1}{2}$BE•EF=5,S△BCF=$\frac{1}{2}$BC•CF=$\frac{1}{2}×4×3$=6于是得到$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{6}$,故④错误.
解答 解:在正方形ABCD中,
∵AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,
∵点E为AD中点,DF=$\frac{1}{4}$CD,
∴$\frac{AB}{DE}=\frac{AE}{DF}$=2,
∴△ABE∽△DEF,
∴∠ABE=∠DEF,
∵∠AEB+∠ABE=90°,
∴∠AEB+∠DEF=90°,
∴∠BEF=90°,
∴BE⊥EF;故①正确;
∵△ABE∽△DEF,
∴$\frac{AB}{DE}=\frac{BE}{EF}$,
∴$\frac{AB}{AE}=\frac{BE}{EF}$,
∵∠A=∠BEF=90°,
∴△ABE∽△BEF,
∴△ABE∽△BEF∽△DEF,
∴图中有3对相似三角形;故②正确;
∵△ABE∽△BEF,
∴∠ABE=∠EBF,
∴E到BF的距离=AE,
∴E到BF的距离为$\frac{1}{2}$AB;故③正确;
设DF=1,则AE=DE=2,AB=BC=CD=4,
∴CF=3,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=2$\sqrt{5}$,EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{5}$,
∴S△BEF=$\frac{1}{2}$BE•EF=5,S△BCF=$\frac{1}{2}$BC•CF=$\frac{1}{2}×4×3$=6
∴$\frac{{S}_{△BEF}}{{S}_{△BCF}}$=$\frac{5}{6}$,故④错误,
故选B.
点评 本题考查了相似三角形的判定和性质,勾股定理,正方形的性质,三角形的面积的计算,熟练掌握相似三角形的判定定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
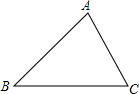 如图,已知△ABC中,AC=6,∠ABC=45°.
如图,已知△ABC中,AC=6,∠ABC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC,
已知∠BOC=30°,OM平分∠AOC,ON平分∠BOC,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 正确字数x | 人数 |
| A | 0≤x<10 | 10 |
| B | 10≤x<20 | 15 |
| C | 20≤x<30 | 25 |
| D | 30≤x<40 | m |
| E | 40≤x<50 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$,且△ABC的面积与△ADE的面积差是15cm2,
如图,$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{2}{3}$,且△ABC的面积与△ADE的面积差是15cm2,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A(-2,m),B(5,-2)两点,与x轴交于C点,过A作AD⊥x轴于D.
如图,一次函数y=ax+b的图象与反比例函数$y=\frac{k}{x}$的图象交于A(-2,m),B(5,-2)两点,与x轴交于C点,过A作AD⊥x轴于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
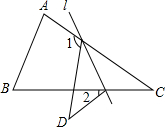 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )| A. | 40° | B. | 80° | C. | 90° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,以(6,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B和C,解答下列问题:
如图,在平面直角坐标系中,以(6,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B和C,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com