
科目: 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOE=∠DOF=90°,OP是∠BOC的平分线,∠AOD=40°.
(1)求∠EOP的度数;
(2)写出∠AOD的补角和余角.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为a的正方形上剪去一个边长为b的小正方形(a>b),把剩下的部分剪拼成一个梯形,分别计算这两个图形阴影部分的面积,由此可以验证的等式是( )

A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0). 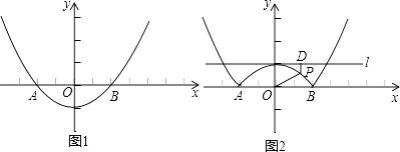
(1)求抛物线的解析式;
(2)若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由. (注:在解题过程中,如果你觉得有困难,可以阅读下面的材料)
附阅读材料:
① 在平面直角坐标系中,若A、B两点的坐标分别为A(x1 , y1),B(x2 , y2),则A,B两点间的距离为|AB|= ![]() ,这个公式叫两点间距离公式.
,这个公式叫两点间距离公式.
例如:已知A,B两点的坐标分别为(﹣1,2),(2,﹣2),则A,B两点间的距离为|AB|= ![]() =5.
=5.
② 因式分解:x4+2x2y2+y4=(x2+y2)2 .
查看答案和解析>>
科目: 来源: 题型:
【题目】张老师要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛” ![]() 为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
为此,他对两位同学进行了辅导,并在辅导期间测验了10次,测验成绩如下表:
第1次 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
甲 | 68 | 80 | 78 | 79 | 78 | 84 | 81 | 83 | 77 | 92 |
乙 | 86 | 80 | 75 | 83 | 79 | 80 | 85 | 80 | 77 | 75 |
利用表中数据,解答下列问题:
![]() 填空完成下表:
填空完成下表:
平均成绩 | 中位数 | 众数 | |
甲 | 80 |
| |
乙 | 80 | 80 |
![]() 张老师从测验成绩表中,求得甲的方差
张老师从测验成绩表中,求得甲的方差![]() ,请你计算乙10次测验成绩的方差.
,请你计算乙10次测验成绩的方差.
![]() 请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
请你根据上面的信息,运用所学统计知识,帮张老师选拔出参加“全国数学联赛”的人选,并简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“五一”假期,成都某公司组织部分员工分别到甲、乙、丙、丁四地考察,公司按定额购买了前往各地的车票,如图是用来制作完整的车票种类和相应数量的条形统计图,根据统计图回答下列问题:
![]() 若去丙地的车票占全部车票的
若去丙地的车票占全部车票的![]() ,则总票数为______ 张,去丁地的车票有______ 张
,则总票数为______ 张,去丁地的车票有______ 张![]()
![]() 若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张
若公司采用随机抽取的方式发车票,小胡先从所有的车票中随机抽取一张![]() 所有车票的形状、大小、质地完全相同、均匀
所有车票的形状、大小、质地完全相同、均匀![]() ,那么员工小胡抽到去甲地的车票的概率是多少?
,那么员工小胡抽到去甲地的车票的概率是多少?
![]() 若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李
若有一张车票,小王和小李都想要,他们决定采取掷一枚质地均匀的正方体骰子的方式来确定给谁,其上的数字是3的倍数,则给小王,否则给小李![]() 请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.
请问这个规则对双方是否公平?若公平请说明理由;若不公平,请通过计算说明对谁更有利.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PAPC,连接CE,AE,OE,OE交CA于点D. 
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP= ![]() AC,求证:DO=DP.
AC,求证:DO=DP.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,顶点为M的抛物线y=a(x+1)2﹣4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】.某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量![]() 单位:吨
单位:吨![]() ,并将调查数据进行如下整理:
,并将调查数据进行如下整理:

频数分布表
分组 | 划记 | 频数 |
| 正正 | 11 |
|
| 19 |
| ||
合计 |
| 2 50 |
![]() 把上面频数分布表和频数分布直方图补充完整;
把上面频数分布表和频数分布直方图补充完整;
![]() 从直方图中你能得到什么信息?
从直方图中你能得到什么信息? ![]() 写出两条即可
写出两条即可![]() ;
;
![]() 为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按
为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按![]() 倍价格收费,若要使
倍价格收费,若要使![]() 的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com