
科目: 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=( )
A.1:16
B.1:18
C.1:20
D.1:24
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 | 跳绳次数 | 频数 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合计 | 50 | |
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(1,0)、B(11,0),点C为线段AB上一动点,以AC为直径的⊙D的半径DE⊥AC,△CBF是以CB为斜边的等腰直角三角形,且点E、F都在第四象限,当点F到过点A、C、E三点的抛物线的顶点的距离最小时,该抛物线的解析式为 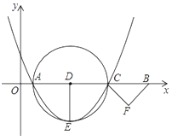
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代对勾股定理有深刻的认识.
(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求(a+b)2的值;
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
=k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.


查看答案和解析>>
科目: 来源: 题型:
【题目】做如下操作:在等腰三角形ABC中,AB= AC,AD平分∠BAC,交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的象与△ACD重合.
对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;
③等腰三角形的顶角平分线、底边上的中线和高互相重合.
由上述操作可得出的是 ▲ (将正确结论的序号都填上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com