A. 2 B. 1 C. D.

【题目】如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（ ）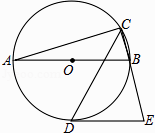
A.
B.2
C.2
D.3

某校师生捐书种类情况统计表

（1）统计表中的m= ，n= ；

（2）补全条形统计图；

（3）本次活动师生共捐书2000本，请估计有多少本科普类图书？

12=；12+22=；12+22+32=；12+22+32+42=；…

①根据你发现的规律，计算下面算式的值；12+22+32+42+52=____________；

②请用一个含n的算式表示这个规律：12+22+32…+n2=___________；

③根据你发现的规律，计算下面算式的值：512+522+…+992+1002=____________．

13+23=1+8=9，而（1+2）2=9，∴13+23=（1+2）2；

13+23+33=36，而（1+2+3）2=36，∴13+23+33=（1+2+3）2；

13+23+33+43=100，而（1+2+3+4）2=100，∴13+23+33+43=（1+2+3+4）2；

∴13+23+33+43+53=（______ ）2= ______ ．

根据以上规律填空：

（1）13+23+33+…+n3=（______ ）2=[ ______ ]2．

（2）猜想：113+123+133+143+153= ______ ．

②一①得：3S―S＝39－1，即2S＝39－1，

∴S＝.

得出答案后，爱动脑筋的张红想：如果把“3”换成字母m（m≠0且m≠1），能否求出1＋m＋m2＋m3＋m4＋…＋m2016的值？如能求出，其正确答案是___________.

【题目】如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c与x轴只有一个交点M，与平行于x轴的直线l交于A、B两点，若AB=3，则点M到直线l的距离为（ ）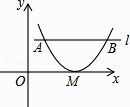
A.
B.
C.2
D.

【题目】如图，在矩形ABCD中，点O为对角线AC、BD的交点，点E为BC上一点，连接EO，并延长交AD于点F，则图中全等三角形共有（ ）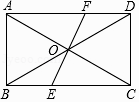
A.5对
B.6对
C.8对
D.10对

【题目】一个袋子中装有3个红球和2个黄球，这些球的形状、大小．质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是（ ）
A.
B.
C.
D.

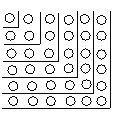
（1）图中的小圆圈被折线隔开分成六层，第一层有1个小圆圈，第二层有3个圆圈，第三层有5个圆圈，……，第六层有11个圆圈.如果要你继续

下去，那么第七层有几个小圆圈？第n层呢？

（2）某一层上有77个圆圈，这是第几层？

（3）数图中的圆圈个数可以有多种不同的方法.

比如：前两层的圆圈个数和为（1+3）或22，

由此得，1 + 3 = 22.

同样，

由前三层的圆圈个数和得：1 + 3 + 5 = 32.

由前四层的圆圈个数和得：1 + 3 + 5 + 7 = 42.

由前五层的圆圈个数和得：1 + 3 + 5 + 7 + 9 = 52.

……

根据上述请你猜测，从1开始的n个连续奇数之和是多少？用公式把它表示出来.

（4）计算：1 + 3 + 5 + … + 19的和；

（5）计算：11 + 13 + 15 + … + 99的和.