
科目: 来源: 题型:
【题目】如图,顶点为P(4,﹣4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,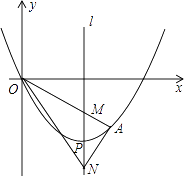
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,﹣3),求△ANO的面积;
(3)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),在矩形ABCD中,把∠B、∠D分别翻折,使点B、D恰好落在对角线AC上的点E、F处,折痕分别为CM、AN, 
(1)求证:△ADN≌△CBM;
(2)请连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图(2)所示,若PQ=CQ,PQ∥MN,且AB=4cm,BC=3cm,求PC的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形网格中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),结合所给的平面直角坐标系解答下列问题: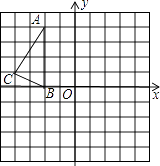
(1)画出△ABC关于原点O对称的△A1B1C1;
(2)平移△ABC,使点A移到点A2(0,2),画出平移后△A2B2C2并写出点B2、C2的坐标;
(3)在△ABC、△A1B1C1、△A2B2C2中,△A2B2C2与成中心对称,其对称中心坐标为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某校有学生2100人,在“文明我先行”活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了100名学生,并制成统计表:校本课程意向统计表
课程类型 | 频数 | 频率(%) |
法律 | s | 0.08 |
礼仪 | a | 0.20 |
环保 | 27 | 0.27 |
感恩 | b | m |
互助 | 15 | 0.15 |
合计 | 100 | 1.00 |
请根据统计表的信息,解答下列问题;
(1)在这次调查活动中,学校采取的调查方式是(填写“普查”或“抽样调查”);
(2)a= , b= , m=;
(3)如果要画“校本课程报名意向扇形统计图”,那么“礼仪”类校本课程对应的扇形圆心角的度数是;
(4)请你估计,选择“感恩”类校本课程的学生约有人.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了进一步推进海南国际旅游岛建设,海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》,第八条规定:“旅行社引进会议规模达到200人以上,入住本市A类旅游饭店,每次会议奖励2万元;入住本市B类旅游饭店,每次会议奖励1万元.”某旅行社5月份引进符合奖励规定的会议共18次,得到28万元奖金,求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次?
查看答案和解析>>
科目: 来源: 题型:
【题目】星期六,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象,根据图象信息,下列说法不一定正确的是( ) 
A.小亮到同学家的路程是3千米
B.小亮在同学家逗留的时间是1小时
C.小亮去时走上坡路,回家时走下坡路
D.小亮回家时用的时间比去时用的时间少
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0),以点P为圆心, ![]() m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图).
m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图). 
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ,试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC﹣∠DBE的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C,D两点).连接PM,过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y.
(1)写出y与x之间的关系式;
(2)若点E与点A重合,则x的值为;
(3)是否存在点P,使得点D关于直线PE的对称点D′落在边AB上?若存在,求x的值;若不存在,请说明理由. 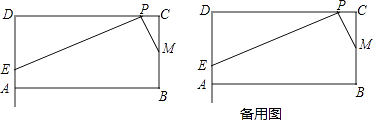
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com