
科目: 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程 ![]() .
.
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线![]() ,则直线
,则直线![]() 与
与![]() 平行.
平行.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】某农业观光园将一块面积为![]() 的观光园分成
的观光园分成![]() 三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲
三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 区域的面积是
区域的面积是![]() 的
的![]() 倍,记A区域的面积为
倍,记A区域的面积为![]() 区域的面积为
区域的面积为![]() .
.
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
|
| |
株/ |
|
|
|
数量 |
|
(1)完成上表(结果用含![]() 的代数式表示).
的代数式表示).
(2)若三种花卉共栽种![]() 株
株
①求![]() 与
与![]() 的值.
的值.
②若三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,求种植面积最大的花卉总价.
元,求种植面积最大的花卉总价.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移4个单位后与反比例函数y= ![]() 在第一象限内的图象交于点P,则k=;△POA的面积为 .
在第一象限内的图象交于点P,则k=;△POA的面积为 . 
查看答案和解析>>
科目: 来源: 题型:
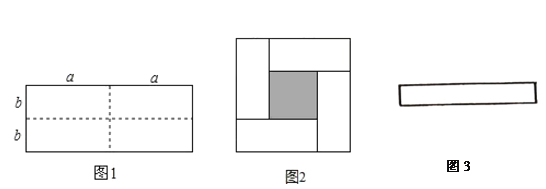
【题目】把一个长为![]() 、宽为
、宽为![]() 的长方形(
的长方形(![]() ),沿图1中虚线用剪刀分成四块相同的小长方形,并将
),沿图1中虚线用剪刀分成四块相同的小长方形,并将![]() 块小长方形彼此不重叠拼成一个正方形(如图2)
块小长方形彼此不重叠拼成一个正方形(如图2)
(1)图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含![]() 的代数式表示).
的代数式表示).
(2)利用图2存在的面积关系,直接写出下列三个代数式![]() 之间的等量关系: .
之间的等量关系: .
(3)如图3,已知长方形的周长为![]() ,面积为
,面积为![]() ,试求该长方形长与宽的差.
,试求该长方形长与宽的差.
查看答案和解析>>
科目: 来源: 题型:
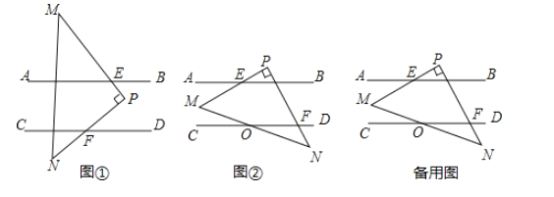
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]()
(1)当![]() 所放位置如图①所示时,则
所放位置如图①所示时,则![]() 与
与![]() 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.
(2)当![]() 所放位置如图②所示时,
所放位置如图②所示时,![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(3)在(2)的条件下,若![]() 与
与![]() 交于点0,且
交于点0,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
![]()
查看答案和解析>>
科目: 来源: 题型:
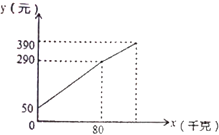
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数![]() 与他手中持有的钱数
与他手中持有的钱数![]() 元(含备用零钱)的关系如图所示,结合图象回答下列问题:
元(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是390元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com