
科目: 来源: 题型:
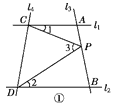
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
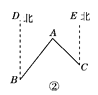
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
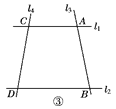
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某小区①号楼与号楼隔河相望,李明家住在①号楼,他很想知道号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算号楼的高度CD. 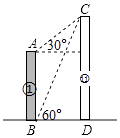
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:
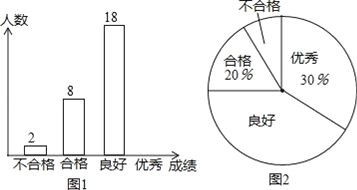
(1)本次接收随机抽样调查的男生人数为 人,扇形统计图中“良好”所对应的圆心角的度数为 ;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布的扇形统计图,其中八年级学生人数为408人,下表是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
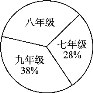
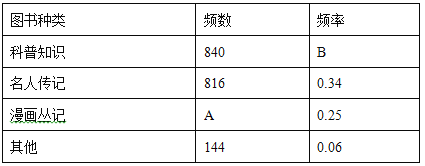
A. 2本 B. 3本 C. 4本 D. 5本
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目: 来源: 题型:
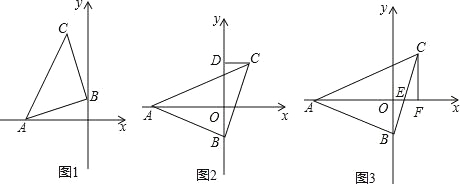
【题目】已知,△ABC 是等腰直角三角形,BC=AB,A 点在 x 负半轴上,直角顶点 B 在 y 轴上,点 C 在 x 轴上方.
(1)如图1所示,若A的坐标是(﹣3,0),点 B的坐标是(0,1),求点 C 的坐标;
(2)如图2,过点 C 作 CD⊥y 轴于 D,请直接写出线段OA,OD,CD之间等量关系;
(3)如图3,若 x 轴恰好平分∠BAC,BC与 x 轴交于点 E,过点 C作 CF⊥x 轴于 F,问 CF 与 AE 有怎样的数量关系?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:
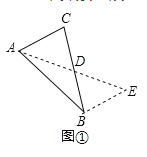

如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com