
科目: 来源: 题型:
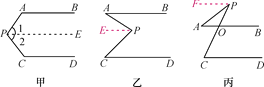
【题目】阅读下列解答过程:(1)如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
(2)如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目: 来源: 题型:
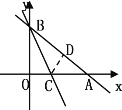
【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.
例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A, C的“联盟点”.
![]()
(1)若点A表示数-2, 点B表示的数2,下列各数![]() ,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
,0,4,6所对应的点分别C1,C2 ,C3 ,C4,其中是点A,B的“联盟点”的是 ;
(2)点A表示数-10, 点B表示的数30,P在为数轴上一个动点:
①若点P在点B的左侧,且点P是点A, B的“联盟点”,求此时点P表示的数;
②若点P在点B的右侧,点P,A, B中,有一个点恰好是其它两个点的“联盟点”,写出此时点P表示的数 .
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代有二十四节气歌,“春雨惊春清谷天,夏满芒夏暑相连.秋处露秋寒霜降,冬雪雪冬小大寒.”它是为便于记忆我国古时历法中二十四节气而编成的小诗歌,流传至今.节气指二十四时节和气候,是中国古代订立的一种用来指导农事的补充历法,是中国古代劳动人民长期经验的积累和智慧的结晶.其中第一个字“春”是指立春,为春季的开始,但在气象学上的入春日是有严格定义的,即连续5天的日平均气温稳定超过10℃又低于22℃,才算是进入春天,其中,5天中的第一天即为入春日.例如:2014年3月13日至18日,北京的日平均气温分别为9.3℃,11.7℃,12.7℃,11.7℃,12.7℃和12.3℃,即从3月14日开始,北京日平均气温已连续5天稳定超过10℃,达到了气象学意义上的入春标准.因此可以说2014年3月14日为北京的入春日. 日平均温度是指一天24小时的平均温度.气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温(即4个气温相加除以4),结果保留一位小数.
如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温(单位:℃)
时间 | 2时 | 8时 | 14时 | 20时 | 平均气温 |
3月28日 | 6 | 8 | 13 | 11 | 9.5 |
3月29日 | 7 | 6 | 17 | 14 | a |
3月30日 | 7 | 9 | 15 | 12 | 10.8 |
3月31日 | 8 | 10 | 19 | 13 | 12.5 |
4月1日 | 8 | 7 | 18 | 15 | 12 |
4月2日 | 11 | 7 | 22 | 16 | 14 |
4月3日 | 13 | 11 | 21 | 17 | 15.5 |
根据以上材料解答下列问题:
(1)求出3月29日的日平均气温a;
(2)采用适当的统计图将这7天的日平均气温的变化情况表示出来;
(3)请指出2017年的哪一天是北京顺义在气象学意义上的入春日.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月17日世界人工智能大会在上海召开,人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一部分.
排名 | 代表队 | 场次 (场) | 胜 (场) | 平 (场) | 负 (场) | 净胜球 (个) | 进球 (个) | 失球 (个) | 积分 (分) |
1 | A | 6 | 1 | 6 | 12 | 6 | 22 | ||
2 | B | 6 | 3 | 2 | 1 | 0 | 6 | 6 | 19 |
3 | C | 6 | 3 | 1 | 2 | 2 | 9 | 7 | 17 |
4 | D | 6 | 0 | 0 | 6 | m | 5 | 13 | 0 |
(说明:积分=胜场积分+平场积分+负场积分)
(1)D代表队的净胜球数m= ;
(2)本次决赛中,胜一场积 分,平一场积 分,负一场积 分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.
请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目: 来源: 题型:
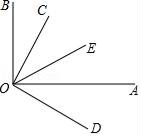
【题目】填空,完成下列说理过程
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连接BC,∠P=∠B. 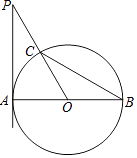
(1)求∠P的度数;
(2)连接PB,若⊙O的半径为a,写出求△PBC面积的思路. 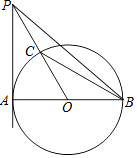
查看答案和解析>>
科目: 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为: ;
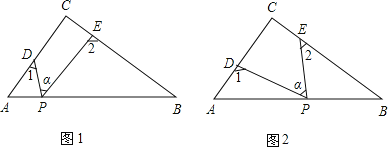
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
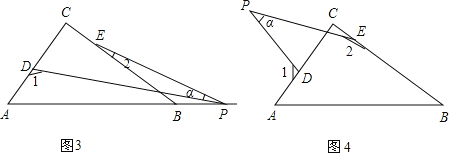
(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为: .
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com